|
機械設計のための基礎製図 第3章 基礎作図
正多角形の作図
以下，多角形を作図する2つの方法(1)を紹介する。
 方法@
【例題】円周を7等分し，正7角形を作図しなさい（付図3.1参照）。
(1) 直径ABの円を作図する。
(2) 直径ABを7等分し，その等分点を1，2，・・・，6とする。
(3) コンパスを使って，AB=AC=BCとなる点Cを求める（△ABCは正三角形）。
(4) 点Cと点2を結び，その延長線と円とが交わる点をDとする。
(5) 辺ADは円周を7等分する基準長さとなるので，円周を7等分できる。
(6) 正7角形を作図する。
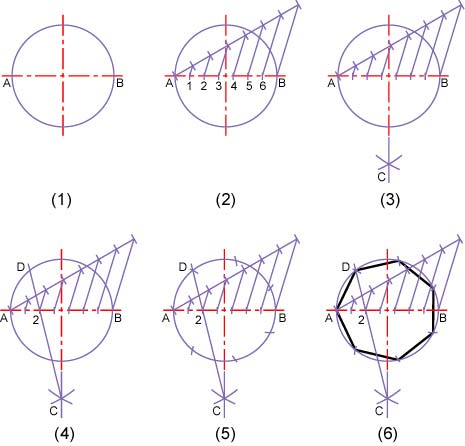
付図3.1 正7角形の作図
【補足】同様の作図法で，直径ABをn等分すれば，正n角形を作図できる。付図3.2は正9角形及び正5角形を作図した例である。ただし，n=3，4，6以外は近似法である。
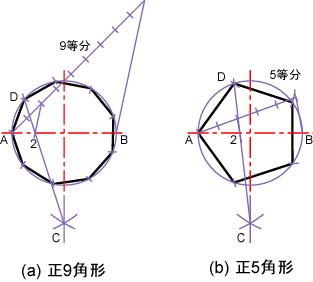
付図3.2 正9角形と正5角形の作図
方法A
【例題】与えられた1辺の長さより，正7角形を作図しなさい（付図3.3参照）。
(1) 線分ABを作図する。
(2) 線分ABを底辺とする正三角形の頂点Cを求める。
(3) 円弧OBを6等分して，各等分点を1，2，・・・，5とする。
(4) C1=COとなるように，点Oを求める。
(5) 点Oを中心とし，点A及び点Bを通る円は正7角形の外接円となるので，正7角形の頂点が求まる。
(6) 正7角形を作図する。
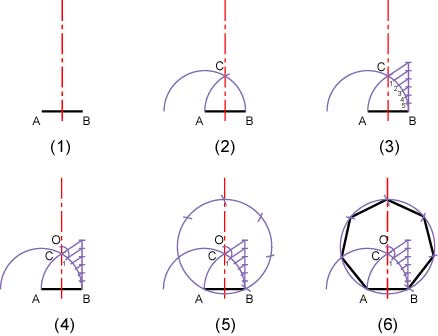
付図3.3 正7角形の作図
【補足】付図3.4に示すように，同様の作図法によって，C1=C7，C2=C8，C5=C10，C6=C12となるように点7，点8，点10，点12を求めれば，様々な正多角形を作図できる。ただし，n=6，12以外は近似法である。
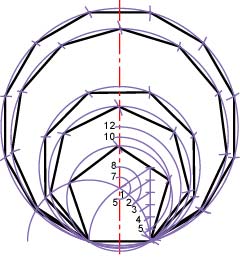
付図3.4 正多角形の作図
参考文献
(1) 岩井実，石川義雄，喜山宣志明，第三角法図学，p.10-11，森北出版(1986)．
| 
