|
機械設計のための基礎製図
第3章 基礎作図
 3.1 用器画法について 3.1 用器画法について
用器画法とは,線分や円周の等分や正多角形,様々な曲線を作図する方法である。昨今,コンピュータを利用した設計・製図(CAD)が普及しているため,手書きで製図を描いていたときと比べて,よりも用器画法の必要性は少なくなっている。しかし,機械工学を学ぶ学生として基本的かつ常識的な作図法はしっかりと習得しなければならない。本章では,今後の講義における課題作成に役立つ基本的な作図法を習得する。さらに,今後の投影法(機械製図)の理解に役立つ正弦曲線(サインカーブ)を作図する。
 3.2 用器画法の例 3.2 用器画法の例
いくつかの代表的な作図法を紹介する。
(1) 直線の作図例
図3.1に示すように,定規やコンパスを使って,定直線や任意の角の2等分線を描くことができる。最も基本的な作図法である。
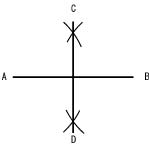
(a) 定直線の2等分線
|
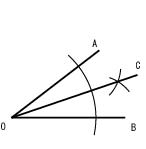
(b) 任意の角の2等分
|
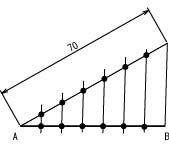
(c) 定直線を任意の数に等分する
|
図3.1 直線の作図例
(2) 円弧の作図例
機械図面において円弧を作図することは極めて多い。例えば,板材に四角い穴をあける場合,エンドミルと呼ばれる円柱形状の工具を使用して加工するため,角の部分は丸くなるのが普通である(図3.2)。
図3.3に示すように,円弧を作図する場合,何らかの方法で円弧の中心(交点)を求めるのが基本である。
|
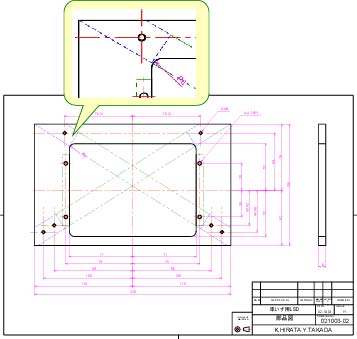
図3.2 円弧を使った機械図面
|
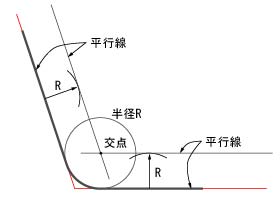
(a) 与えられた半径で任意の角を作る直線に接する円弧を描く
|
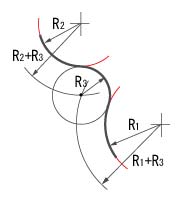
(b) 与えられた半径で2円に接する円弧を描く
|
図3.3 円弧の作図例
(3) 多角形の作図例
機械製図によく出てくる正6角形や正3角形は簡単に作図することができる(図3.4)。また,作図方法はかなり複雑になるが,コンパスと定規を使って任意の正多角形を描くこともできる(図3.5)。
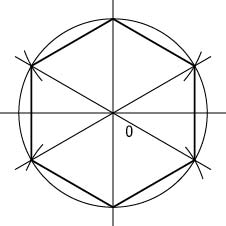
図3.4 正6角形の作図
|
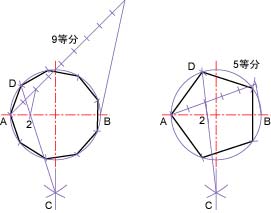
図3.5 正9角形と正5角形の作図例
|
 付録:任意の正多角形の作図方法はこちら
付録:任意の正多角形の作図方法はこちら
(4) 楕円の作図例
やや難しくなるが,用器画法で楕円を作図することもできる(図3.6)。また,円柱を斜めに切断すると楕円ができることも覚えておくとよい。
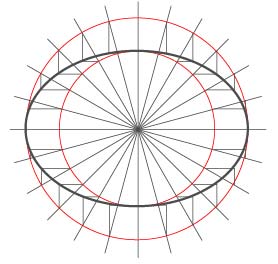
(a) 楕円の作図
|
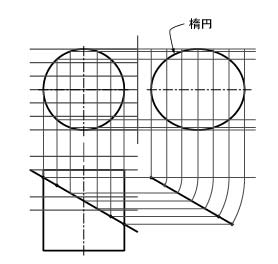
(b)円柱の切断(第7章参照)
|
図3.6 楕円の作図例
(5) 曲線の作図例
曲線には様々な種類があるが,最低限,次の2種類の曲線の定義は頭に入れておきたい。曲線は定義を知っておくことが重要である。
インボリュート曲線:図3.7に示すインボリュート曲線は,「筒に巻き付けた糸を張りながらほどくとき,糸の一端が描く曲線」である。一般機械の歯車に使われている曲線である。

|

図3.7 インボリュート曲線
|
|
サイクロイド曲線:図3.8に示すサイクロイド曲線は,「円が転がるとき,円上の1点が描く曲線 」である。時計などの精密機械の歯車に使われている。
|

図3.8 サイクロイド曲線
|
 CADを使うと・・・ CADを使うと・・・
CADを使った場合,どのような作図ができるのだろうか。以下CAD(Auto CAD LT 2000)による作図について簡単に紹介する。
|
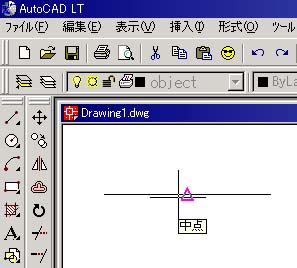 ●「Oスナップ」という機能を使うと,長さを測らなくても中点が簡単に求まる。
●「Oスナップ」という機能を使うと,長さを測らなくても中点が簡単に求まる。
|
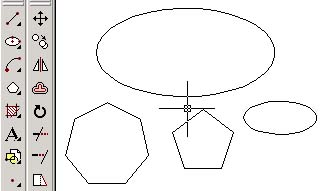 ●正多角形や楕円もとても簡単に作図できる。
●正多角形や楕円もとても簡単に作図できる。
|
 ●「フィレット」という機能を使うと,直線と直線の交点部分に任意の円弧が引ける。なお,「R」は半径を表す記号である。
●「フィレット」という機能を使うと,直線と直線の交点部分に任意の円弧が引ける。なお,「R」は半径を表す記号である。
|
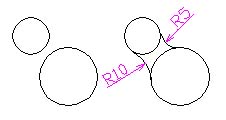 ●円弧と円弧の間に円弧を描く場合にも「フィレット」を利用できる。
●円弧と円弧の間に円弧を描く場合にも「フィレット」を利用できる。
|
このように,CADは作図をするときに非常に便利なツールである。しかし,上述のインボリュート曲線やサイクロイド曲線は,それらの定義を知っていないとCADを使っても作図できない。また,CADが設計や製図をしてくれるのではないので,製図の基本的な知識がないとCADは使えない。
|
 3.3 課題 3.3 課題
 【課題①:定直線の垂直2等分線】
【課題①:定直線の垂直2等分線】
任意の定直線ABを引き,定規で長さを測らずに,垂直2等分線CDを引きなさい。
●教科書p.40,表3-2(1)参照。
●コンパスで引いた補助線及び記号(A,B,C,D)は消しゴムで消さず,残しておくこと。
 【課題②:任意の角の2等分】
【課題②:任意の角の2等分】
任意の角AOBを引き,分度器で角度を測らずに,角AOBを2等分する線OCを引きなさい。(補助線,記号(O,A,B,C)は残しておくこと。)
●教科書p.40,表3-2(4)参照。
●補助線,記号(O,A,B,C)は残しておくこと。
 【課題③:正六角形の作図】
【課題③:正六角形の作図】
次の手順に従って,正六角形を作図しなさい。
(1) 長さ60 mm程度の線及びその垂直2等分線を引く。
(2) 交点を中心として直径50 mm(半径25 mm)の円を描く。
(3) 円と直線との交点を中心として半径25 mmの円弧を描き,(2)で描いた円との交点を求める。
(4) (3)で得られた交点と(2)で描いた円の中心とを結ぶ。
(5) 以上の手順を繰り返し,正六角形の頂点を求め,正六角形を描く。
 【課題④:定直線の等分】
【課題④:定直線の等分】
次の手順に従って,定直線ABを7等分しなさい。
(1) 定直線AB(長さ60 mm程度)を引く。
(2) 定規またはドラフタを使って,長さ70 mm(7で割り切れる長さ)の直線ACを引く。
(3) 直線ACを7等分し,点(黒丸)をつける。
(4) 点Bと点Cを結ぶ直線BCを引く。
(5) 2枚の三角定規を使って,直線BCと平行で,(3)でつけた点を通る直線6本を引く。
(6) (5)で引いた6本の直線と定直線ABとの交点が,定直線ABを7等分している。
●教科書p.40,表3-2(8)参照。
●上の説明をよく読み,課題の主旨をしっかりと理解してから作図すること。
【課題⑤:正弦曲線の作図】
正弦曲線(サインカーブ)とは,等速円運動を横方向から見た軌跡である。次の手順に従って,正弦曲線を作図しなさい。
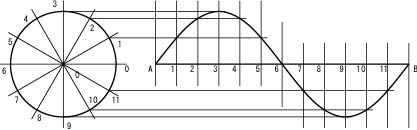 (1) 直径50 mmの円Oを描く。
(1) 直径50 mmの円Oを描く。
(2) 課題③を参考にして,円Oを12等分し,番号0~11をふる。
(3) 円O中心の右に,長さ120 mm直線ABを引く。
(4) ドラフタを使って,点A,Bから垂直線を引く。
(5) 円Oの各点(0~11)から横方向に平行線を引く。
(6) 直線ABを12等分(10mm間隔)し,番号0~11をふる。
(7) 直線ABの各点(0~11)から垂線を引く。
(8) 自在定規または雲形定規を使って,交点を滑らかに結び,正弦曲線を作図する。
●この課題は自在定規を使って曲線を引く練習を兼ねている。滑らかできれいな線が引けるように,しっかりと練習すること。
【課題⑥:インボリュート曲線の作図】
インボリュート曲線とは,丸い筒に糸を巻き付け,糸を引っ張りながらほどいていくとき,糸の先端の軌跡である。以下の手順に従って,インボリュート曲線を作図しなさい。
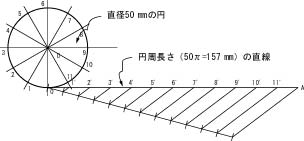 (1) 直交する2本の直線を引き,直径50 mmの円Oを描く。(最終的な図面を考えて,位置を決めること。)
(1) 直交する2本の直線を引き,直径50 mmの円Oを描く。(最終的な図面を考えて,位置を決めること。)
(2) 課題③を参考にして,円Oを12等分し,番号0~11をふる。
(3) 点0から円周分(50π=157 mm)の直線0Aを引く。
(4) 課題④を参考にして,直線0Aを12等分し,番号1'~11'をふる。
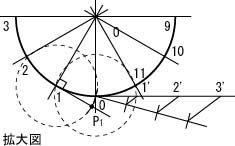 (5) 点1から,直線01に垂直な線を引く。(方法は問わない。)
(5) 点1から,直線01に垂直な線を引く。(方法は問わない。)
(6) コンパスで直線01'の長さをとり,直線点1を中心に円弧を描く。
(7) 円弧と(5)で引いた直線との交点P1を求める。
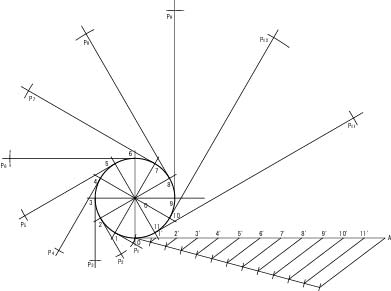 (8) 同様にして,(5)~(7)の手順を点2~点11について繰り返し,点P2~点P11を求める。
(8) 同様にして,(5)~(7)の手順を点2~点11について繰り返し,点P2~点P11を求める。
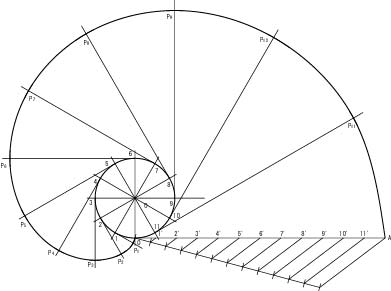 (9) 以上で求められた点0,点P2~点P11,点Aを滑らかな曲線で結ぶ。
(9) 以上で求められた点0,点P2~点P11,点Aを滑らかな曲線で結ぶ。
 配布プリントのPDFファイル(平成14年度)
配布プリントのPDFファイル(平成14年度)
|  3.1 用器画法について
3.1 用器画法について 3.2 用器画法の例
3.2 用器画法の例 付録:任意の正多角形の作図方法はこちら
付録:任意の正多角形の作図方法はこちら 3.3 課題
3.3 課題















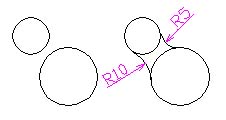
 (1) 直径50 mmの円Oを描く。
(1) 直径50 mmの円Oを描く。 (1) 直交する2本の直線を引き,直径50 mmの円Oを描く。(最終的な図面を考えて,位置を決めること。)
(1) 直交する2本の直線を引き,直径50 mmの円Oを描く。(最終的な図面を考えて,位置を決めること。) (5) 点1から,直線01に垂直な線を引く。(方法は問わない。)
(5) 点1から,直線01に垂直な線を引く。(方法は問わない。) (8) 同様にして,(5)~(7)の手順を点2~点11について繰り返し,点P2~点P11を求める。
(8) 同様にして,(5)~(7)の手順を点2~点11について繰り返し,点P2~点P11を求める。 (9) 以上で求められた点0,点P2~点P11,点Aを滑らかな曲線で結ぶ。
(9) 以上で求められた点0,点P2~点P11,点Aを滑らかな曲線で結ぶ。