講義ノート:もの作りのための機械設計工学
第4章 ねじを使う設計技術
4.3 ねじの強度
ねじは,締め付けるだけでも,軸方向の引張り荷重を受ける。また,使用する場所によっては,機械の運転中にさらに強い力を受けることもある。以下,ねじの強度について考える。
 4.3.1 ねじに作用する荷重とねじの破損
4.3.1 ねじに作用する荷重とねじの破損
ねじが軸方向の荷重を受ける場合,おねじ内部での引張り荷重およびねじ山でのせん断荷重が作用する。また,ねじが軸に垂直な荷重を受ける場合,おねじへのせん断荷重が作用する。まずは概念的にそれらの荷重について考えてみる。
(1) 軸方向の引張り荷重
|
図4.29に示すように,ねじが軸方向の荷重を受ける場合,おねじ内部での引張り荷重が生じる。引張り応力がおねじの引張り強さを越えると,おねじは破断する。また,機械設計時には,ねじを締め付けるだけでも,軸方向の引張り荷重を受けることを注意しておかなければならない。
|
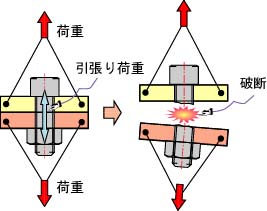
図4.29 軸方向の引張り荷重
|
(2) ねじ山のせん断荷重
|
ねじが軸方向の荷重を受ける場合,おねじとめねじが接している部分では,ねじ山にせん断荷重が生じる(図4.30)。おねじとめねじとが同じ材質の場合,おねじの方がせん断力を受ける面積が小さいので,先に壊れやすい。しかし,高い強度のボルトとアルミニウム合金製部品のめねじとを組み合わせる場合などは,めねじの方が壊れやすくなることがあるので注意する。
|
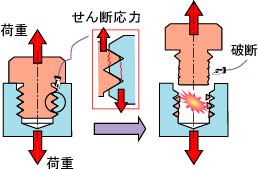
図4.30 ねじ山のせん断荷重
|
(3) ねじへのせん断荷重
通常,ねじには軸と垂直方向の強いせん断荷重や曲げ荷重がかからないようにするのが機械設計の原則である。しかし,実際の機械では,せん断荷重や曲げ荷重がかかる場所に,ボルトなどを使わなくてはならない状況も多い(図4.31)。そのような場合,図4.32に示すように,ねじへのせん断荷重が生じる。自動車の車輪を止めているねじのように,複数のねじでせん断荷重を分散させる場合,ねじが緩むと,1本のねじにせん断荷重が集中するため極めて危険である。

図4.31 せん断荷重がかかるねじ
(魚ロボット尾部のリンク機構)
|
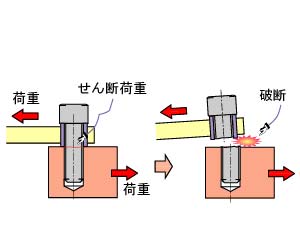
図4.32 軸方向の引張り荷重
|
 ねじへのねじり荷重
ねじへのねじり荷重
やや特殊な例であるが,図4.33に示すように,めねじの深さが十分でない場合,おねじの先端がめねじの下穴の底に当たった状態でおねじを強く締め付けるとおねじに強いねじり荷重が生じる。タップ加工の際,タップの先端が下穴の底に当たっているのに気づかず,さらにタップを回そうとすると簡単に折れてしまう。機械加工の初心者によくある失敗である。
|
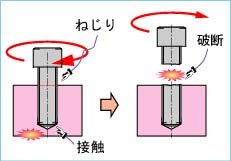
図4.33 ねじり荷重を受けるねじ
|
|
 4.3.2 ねじに使われる材料
4.3.2 ねじに使われる材料
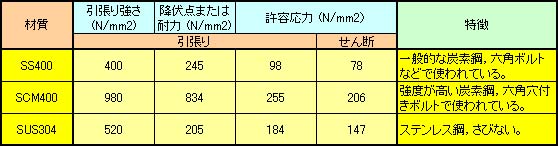
表4.9は,ねじに使われる主な金属材料の強度並びに特徴を示している。表中のSCM440は六角穴付きボルトに使われる材料であり,他の材料と比べてかなり強度が高いことがわかる。なお,鉄鋼材料は熱処理の方法などにより強度が変わるので,表中の値は一つの目安として考えていただきたい。なお,同表の許容応力は静的荷重の場合であり,動的荷重の場合は2/3倍,衝撃荷重の場合は1/3倍程度となる。
表4.9 ねじに使われる材料
 4.3.3 強度計算
4.3.3 強度計算
図4.29,図4.30および図4.32に示したように,ねじが壊れる原因には3種類の荷重がある。しかし,実際の機械において,ねじにはそれらの荷重が複雑に作用するため,詳細な強度計算を行うことは極めて難しい。以下,概念的な強度計算を行うため,3種類の荷重を簡易的に取り扱う。
(1) 軸方向の引張り荷重
図4.29に示した軸方向の荷重F(N)を受けるねじでは許容応力σa(N/mm2)が次式を満たすようにねじを選定する。
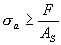 (4.2) (4.2)
ここで,ASはおねじの有効断面積(mm2)である。
 ねじの有効径
ねじの有効径
有効断面積ASはねじの有効径を基準とした断面積である。有効径とはねじ山の幅がねじ溝の幅と等しくなるような仮想的な円筒の直径である。メートルねじの有効径はJISによって決められているが,ここでの詳細な説明は省略する。以下の計算例では,有効径よりもやや小さいおねじの谷の径を基準とした。そのため,荷重は安全側に計算される。強度計算で重要なことは,計算結果が安全側なのか危険側なのかを把握しておくことである。
|
式(4.2)を表4.2のメートル並目ねじの寸法,表4.9の各種金属材料の引張り強さ並びに許容応力に当てはめると,各ねじが破断する荷重(引張り強さに対応する荷重),使用に不具合が生じる荷重(耐力または降伏点に対応)や実際に使用可能な荷重(許容応力に対応)が求められる。
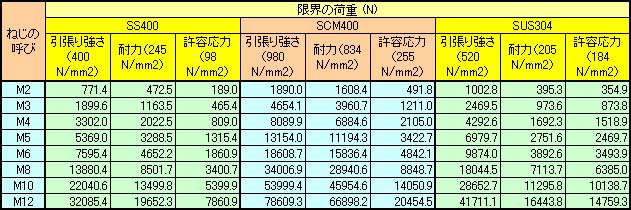
表4.10に有効断面積ASをおねじの谷の径d1を基準とした断面積に置き換えて計算した結果を示す。これより,1本のM3のねじ(SS400)では,465 N(47 kgf)程度の荷重まで使用でき,約1164 N(119 kgf)の荷重で不具合が生じ,約1900 N(194 kgf)の荷重で破断することがわかる。
表4.10 ねじの強度
(2) ねじ山のせん断荷重
|
図4.30に示した軸方向の荷重F(N)を受けるねじにおいて,ねじ山にかかるせん断応力を簡易的に求めてみる。計算を簡単にするため,図4.34に示すようにねじ山の付け根にせん断荷重が加わるものと仮定すると,図中の長さABおよびCDはピッチP(mm)に等しくなる。したがって,おねじがせん断荷重を受ける面積SB(mm2)およびめねじがせん断荷重を受ける面積SN(mm2)は次式で求められる。
|
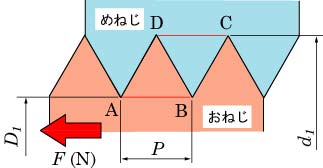
図4.34 軸方向の荷重によりせん断荷重を受けるねじ山
|
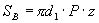 (4.3) (4.3)
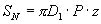 (4.4) (4.4)
ここで,d1はおねじの谷の径(mm),D1はめねじの谷の径(mm)である。zはおねじとめねじとがかみ合うねじ山の数であり,めねじの深さ(またはナットの長さ)をL(mm)とすると近似的に次式で求まる。
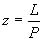 (4.5) (4.5)
したがって,おねじのねじ山にかかるせん断応力τB (N/mm2)およびめねじのねじ山にかかるせん断応力τN(N/mm2)は次式となる。
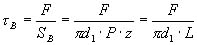 (4.6) (4.6)
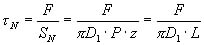 (4.7) (4.7)
式(4.6)および式(4.7)において,D1>d1であるので,τB>τNである。すなわち,おねじとめねじが同じ材料の場合はおねじの方が壊れやすいことがわかる。また,おねじとめねじとがかみ合うねじ山の数が多いほど強度が高まることがわかる。以上の式および表4.2や表4.6のメートル並目ねじおよびナットの寸法,表4.9の各種金属材料のせん断許容応力を利用することで,ねじの大きさや本数,あるいはめねじの深さなどを求めることができる。なお,実際のねじでは,おねじとめねじの間にわずかな隙間があるため,図4.34における長さABおよびCDは短くなる(雄ねじで0.75倍,めねじで0.875倍)。
(3) ねじへのせん断荷重
図4.32に示すように,ねじへのせん断荷重F(N)が生じる場合,おねじにかかるせん断応力τ(N/mm2)は次式で近似される。
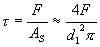 (4.8) (4.8)
式(4.8)を表4.2のメートル並目ねじの寸法並びに表4.9の各種金属材料のせん断許容応力に当てはめると, 1本のM3のねじ(SS400)では,370 N(38 kgf)程度のせん断荷重まで使用できることがわかる。図4.35に示すように複数のねじを使った場合でも,せん断荷重は1本のねじに集中しやすく,また荷重が与えられる位置によってはせん断荷重が増加することもあるので,設計時には気をつけなければならない。
|
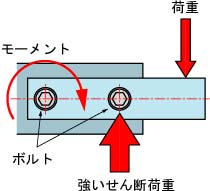
図4.35 せん断荷重を受けるねじ
|
|  4.3.1 ねじに作用する荷重とねじの破損
4.3.1 ねじに作用する荷重とねじの破損 4.3.2 ねじに使われる材料
4.3.2 ねじに使われる材料
 4.3.3 強度計算
4.3.3 強度計算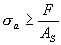 (4.2)
(4.2)
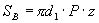 (4.3)
(4.3)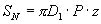 (4.4)
(4.4)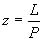 (4.5)
(4.5)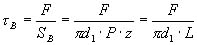 (4.6)
(4.6)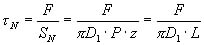 (4.7)
(4.7)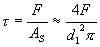 (4.8)
(4.8)



 ねじへのねじり荷重
ねじへのねじり荷重

