講義ノート:もの作りのための機械設計工学
第9章 機械システム設計
9.5 高速化を目指した魚ロボットの設計
本節では,魚ロボットを高速化するための方法について検討し,高速化を目指して設計した実験用魚ロボットを紹介する。さらに,実験用魚ロボットの尾ひれの周波数や振幅が遊泳速度および消費電力に及ぼす影響を測定し,設計計算法の妥当性について検討する。
 実験用魚ロボット「PF-700」 実験用魚ロボット「PF-700」
 9.5.1 魚ロボットを高速化する方法
9.5.1 魚ロボットを高速化する方法
|
現在までに基本特性が測定されている魚ロボットの実験結果に基づき,魚ロボットを高速化する方法について検討する。図9.29は,今までに開発された魚ロボットの構造および実験結果の一例を示している。これより,魚ロボットの速度は,尾ひれの周波数の上昇に伴って増加していることがわかる。また,図9.29の魚ロボットはラジコン模型用サーボモータによって尾部を駆動している。しかし,サーボモータは回転速度と最大トルクの制限により尾ひれを高い周波数で運動させることは難しい。以上の考察より,本節で設計・試作する魚ロボットの尾部の駆動源には,高回転・高出力が得られる回転式直流モータ(図8.1)を使用し,尾ひれの周波数を高めることとした。
|
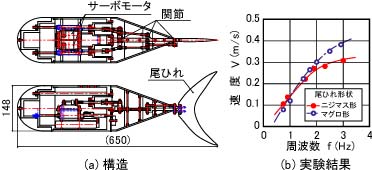
図9.29 今までに開発した魚ロボット
|
|
一方,魚ロボットを高速化するためには,水の流体抵抗による損失を低減する必要がある。そのためには,前方投影面積が小さく,進行方向に細長い体形が適していると考えられた。そこで,実験用魚ロボットの形状は,図9.30に示すサンマの形状を参考にすることとした。
|
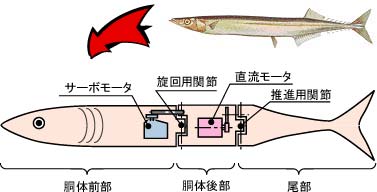
図9.30 魚ロボットのモデル
(参考:学研の図鑑 魚,学研(1998))
|
 9.5.2 実験用魚ロボットの設計
9.5.2 実験用魚ロボットの設計
|
実験用魚ロボットの寸法並びに駆動源や駆動機構の仕様を決定するに当たって,尾部の最高速度・最大荷重に着目した簡易的な設計計算を行った。図9.31の計算モデルに示すように振動する尾部を1枚の平板と仮定すると,関節に作用する最大トルクおよび出力(仕事率)は以下のように求められる。
|
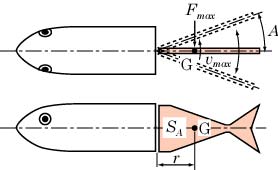
図9.31 設計計算モデル
|
平板の重心をGとし,点Gの最高速度vmaxを次式で近似する。
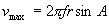 (9.1) (9.1)
ここで,fは尾ひれの周波数(Hz),rは関節から重心Gまでの回転半径(m),Aは振幅(deg)である。
重心Gに作用する最大荷重Fmaxは平板の面積SAを用いて次式で算出される。
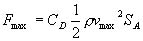 (9.2) (9.2)
ここで,CDは抵抗係数(=1.2),ρは水の密度(=1000 kg/m3)である。
したがって,関節に作用する最大トルクTqmaxおよび最大出力Wmaxは次式で求められる。
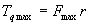 (9.3) (9.3)
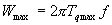 (9.4) (9.4)
|
図9.32は,最終的に決定した実験用魚ロボットの寸法(SA=108.8 cm2,r=95 mm)に基づき,振幅Aを5,10および15 degとした場合の周波数fに対する最大トルクTqmaxおよび最大出力Wmaxの計算結果を示している。同図には,駆動機構の減速比dをパラメータとした場合の直流モータ(マブチモータ製,540SH-7520)のトルク・出力特性を併記している。なお,モータ特性はカタログを参考にして推測した値である(表8.2)。同図において,最大トルクTqmaxおよび最大出力Wmaxの計算結果が直流モータの特性を下回る範囲が,尾部の駆動可能範囲である。また,直流モータの最大出力時の回転数は約8000 rpm(133 Hz),最高効率時の回転数は13000 rpm(217 Hz)であり,その範囲で運転することが望ましい。以上の計算結果および駆動機構の構造等を踏まえて,減速比dを1/16.7とし,尾部を最高8〜13 Hz程度の周波数で振動させることとした。 |
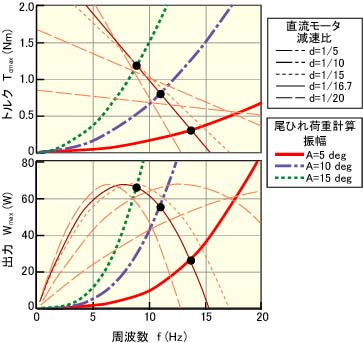
図9.32 計算結果
|
 9.5.3 実験用魚ロボットの構造
9.5.3 実験用魚ロボットの構造
|
図9.33および図9.34は,以上の検討結果に基づき試作した魚ロボットの外観および構造を示している。本魚ロボットは,胴体前部,胴体後部および尾部から構成されており,回転式直流モータで尾部を振動させることにより推進力を発生し,旋回用サーボモータにより進路調整(旋回)を行う。
|

図9.33 魚ロボットの外観
|
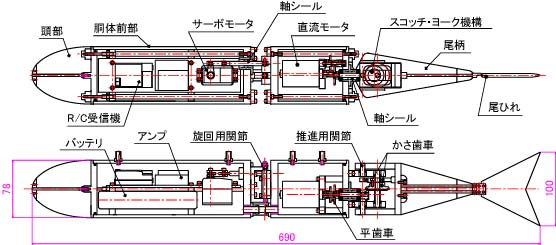
図9.34 魚ロボットの構造
胴体前部の内部にはR/C受信機,直流モータ用アンプ,バッテリおよび旋回用サーボモータが配置されている(図9.35)。旋回用サーボモータにつなげられたロッドは市販のすべり軸受によってシールされ,胴体後部に接続される。胴体後部には,直流モータと減速機構の平歯車が配置されている(図9.36)。胴体前部のアンプと直流モータとの配線はシリコンゴム製のホースにより防水されている。減速機構は4段の平歯車および回転方向を変えるための1組のかさ歯車で構成されている。回転運動を往復運動に変換する機構には,スコッチ・ヨーク機構が用いている。スコッチ・ヨーク機構は小型化が可能であるため,サンマのような細長い体形に適合しやすいと考えられたためである。

図9.35 胴体内部の部品
|
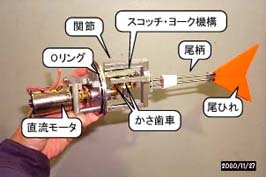
図9.36 尾ひれの駆動部
|
 9.5.4 実験用魚ロボットの性能
9.5.4 実験用魚ロボットの性能
|
魚ロボットを試作した後,長さ10 m,幅3 m,深さ1 mの水槽で実験を行った。図9.37は,尾ひれの振幅Aを5,10および15 degとした場合の周波数fと速度Vの関係を示している。これより,速度Vは,周波数fが高く,振幅Aが大きくなるに従って増加していることがわかる。本実験において,魚ロボットの最高速度は,振幅A=10 deg,周波数f=11 Hzのとき,約0.68 m/sであった。これは,概ね1秒間に魚ロボットの全長とほぼ同じ距離を進む速度であり,実際の魚と比べると決して速いとは言えない。しかし,図9.29に示した魚ロボットの速度の約2倍に達しており,尾ひれの周波数を高めることは魚ロボットの高速化に有効であることが確認された。
|
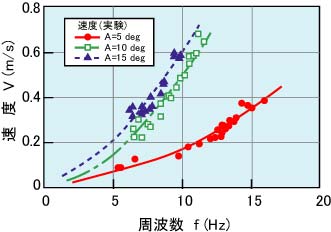
図9.37 周波数と速度の関係
|
図9.32の設計計算において,尾ひれの振幅が5 degの場合には約13 Hz以下,10 degの場合は約10 Hz以下および15 degの場合は約9 Hz以下の周波数で運動できると予測された。本実験結果は,計算結果をやや上回っているものの,概ね設計計算の結果と一致しており,本報で述べた計算法は駆動源および駆動機構の仕様を決定する際に有用であると考えられる。
|
図9.38は,尾ひれの振幅Aを5,10および15 degとした場合の周波数fと消費電力Weの関係を示している。同図には,式(9.1)〜(9.4)において最高速度vmaxを平均速度に置き換えて計算した平均出力Wmを併記している。実測の消費電力Weは尾部を振動させるためのエネルギー(計算値に相当)に駆動機構の損失を加えたものになるが,本実験結果は計算による平均出力Wmと同程度である。すなわち,本節に述べた計算法により,大まかな消費電力を推定できるものと考えられ,今後の魚ロボットの設計に有効であると考えられる。
|
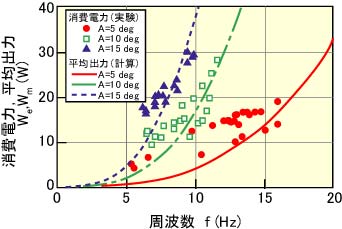
図9.38 周波数と消費電力,平均出力の関係
|
 9.5.5 まとめ
9.5.5 まとめ
9.4節で紹介した魚ロボットと同様,与えられた問題に対する解決手段を考えることが重要である。本魚ロボットの設計においては,魚ロボットを高速化する方法について検討している。また,出力の計算と消費電力の測定からもわかるように,簡易的な計算であっても機械設計に役立つことがわかる。システム設計においては,必要に応じたレベルの設計計算を行いたい。もちろん,実機における魚ロボット周りの水の流れと計算における仮定とは大きく異なっているのは明らかであり,魚ロボットの詳細な特性を見積もるためには,水の流れを考慮した解析が必要である。
|  9.5.1 魚ロボットを高速化する方法
9.5.1 魚ロボットを高速化する方法 9.5.2 実験用魚ロボットの設計
9.5.2 実験用魚ロボットの設計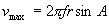 (9.1)
(9.1)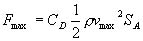 (9.2)
(9.2)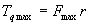 (9.3)
(9.3)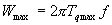 (9.4)
(9.4) 9.5.3 実験用魚ロボットの構造
9.5.3 実験用魚ロボットの構造
 9.5.4 実験用魚ロボットの性能
9.5.4 実験用魚ロボットの性能 9.5.5 まとめ
9.5.5 まとめ 実験用魚ロボット「PF-700」
実験用魚ロボット「PF-700」







