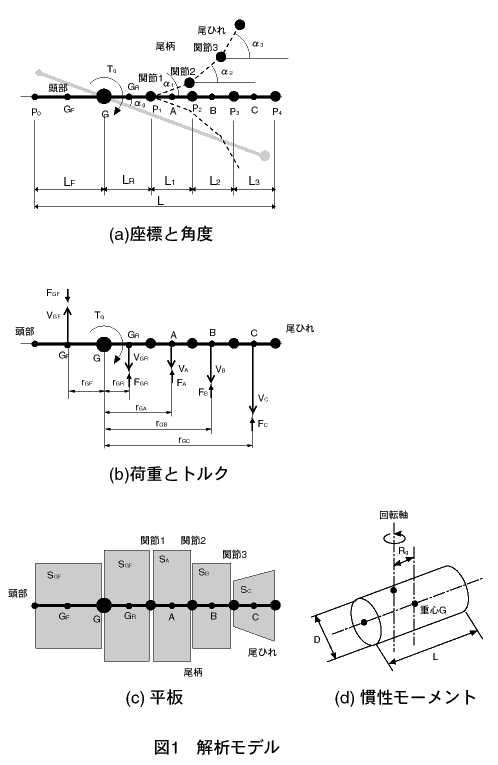
 右の図に解析モデルを示します。同図に示すように、魚ロボットを5つの平板に分割します。
右の図に解析モデルを示します。同図に示すように、魚ロボットを5つの平板に分割します。
1998/10/12 平田宏一
 右の図に解析モデルを示します。同図に示すように、魚ロボットを5つの平板に分割します。
右の図に解析モデルを示します。同図に示すように、魚ロボットを5つの平板に分割します。
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
ここでαgは重心回りの角度であり、その計算方法については後述します。α1、α2およびα3は、それぞれ関節1、関節2および関節3の角度であり、関節1と関節2とは同位相で運動し、関節3の運動はそれらに対してΔαの位相遅れがあるとした場合、次式で与えられます。
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
ここでα1max、α2maxおよびα3maxは、それぞれ関節1、関節2および関節3の最大角度です。位相θは角速度ω=dθ/dt(rad/sec)、時間t(sec)および周波数f(Hz)と次の関係があります。
![]() (14)
(14)
平板に作用する荷重は、P0〜P4の中点に働くものと仮定します。それら中点の座標は式(1)〜(14)から容易に求めることができます。また、各点の速度Vおよび加速度Aは、式(1)〜(14)を微分することで求められますが、その関係式は極めて複雑になるため、今回は数値解析的に解くこととしました。
![]() (15)
(15)
![]() (16)
(16)
ここで、CDは抵抗係数(=1.2)、ρは密度(=1000 kg/m3)、Sは平板の面積、mは平板の質量です。
![]() (17)
(17)
上式における±は、右回り(時計回り)を+、左回り(反時計回り)を−にとります。
![]() (18)
(18)
![]() (19)
(19)
したがって、各サーボモータの出力E1、E2(W)およびサーボモータの駆動に必要な全出力Etは、周波数f(Hz)を用いて次式で求まります。
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
重心周りの回転運動の計算には、以下の3種類の計算手法を用います。
![]() (23)
(23)
![]() (24)
(24)
ここで、微小時間Δtにおける変位角Δαgは次のように表されます。
![]()
![]() (25)
(25)
Δtは計算上の時間幅を表しており、式(25)から変位角Δαgおよびαgを算出することができます。
一方、重心周りの慣性モーメントIは構成要素の形状と質量から求めることができますが、一次設計の段階で詳細に検討するのは簡単ではありません。したがって、図1(d)に示すような円柱を想定し、次式で求まる慣性モーメントIを参照します。
![]() (26)
(26)
なお、L=1 m、Rg=0 m、ρ=1000 kg/m3とした場合、D=100 mmでI=0.67 Nms2、D=200 mmでI=2.93 Nms2、D=300 mmでI=7.48 Nms2、そしてD=400 mmでI=15.5 Nms2となります。
![]() (27)
(27)
したがって、次の微分方程式を数値解析的に解くことにより、αgを求めることができます。
![]() (28)
(28)
この手法は、エンジンのフライホイルのように一定の回転方向の場合に適用できます。しかし、魚ロボットの場合、回転方向が反転する。式(28)からわかるように、計算において、角速度ωが0に限りなく近づくとき、すなわち重心周りの回転運動が限りなく遅くなるとき、dω/dθは無限大に発散し、ωは急激に加速されることになります。これは計算上の不具合となるため、計算プログラムでは角加速度の最大値を適宜設定し、さらにω=0とならないように計算結果を補正しています。
|
要素 |
名称 |
記号 |
値 |
単位 |
|
主要寸法 |
関節1の最大角度 |
α1max |
20 |
deg |
|
関節2の最大角度 |
α2max |
40 |
deg |
|
|
関節3の最大角度 |
α3max |
30 |
deg |
|
|
尾ひれの位相遅れ |
Δα |
90 |
deg |
|
|
全長 |
L |
1 |
m |
|
|
全重量 |
M |
15L3 |
kg |
|
|
各部長さ |
頭端部−重心 |
LF |
0.40L |
m |
|
重心−関節1 |
LR |
0.17L |
m |
|
|
関節1−関節2 |
L1 |
0.13L |
m |
|
|
関節2−関節3 |
L2 |
0.13L |
m |
|
|
関節3−尾端部 |
L3 |
0.17L |
m |
|
|
各部面積 |
頭端部−重心 |
SGF |
0.080L2 |
m2 |
|
重心−関節1 |
SGR |
0.050L2 |
m2 |
|
|
関節1−関節2 |
SA |
0.023L2 |
m2 |
|
|
関節2−関節3 |
SB |
0.016L2 |
m2 |
|
|
関節3−尾端部 |
SC |
0.026L2 |
m2 |
|
|
各部質量 |
頭端部−重心 |
MGF |
0.2M |
kg |
|
重心−関節1 |
MGR |
0.3M |
kg |
|
|
関節1−関節2 |
MA |
0.2M |
kg |
|
|
関節2−関節3 |
MB |
0.2M |
kg |
|
|
関節3−尾端部 |
MC |
0.1M |
kg |
|
|
計算条件 |
慣性モーメント |
I |
1.5〜20 |
Nms2 |
|
計算繰り返し数 |
Rep |
10 |
cycle |
|
|
計算ステップ |
DegStep |
1 |
deg |
|
|
係数 |
Cd |
1.2 |
||
|
重心周り許容角度 |
αglim |
90 |
deg/cycle |
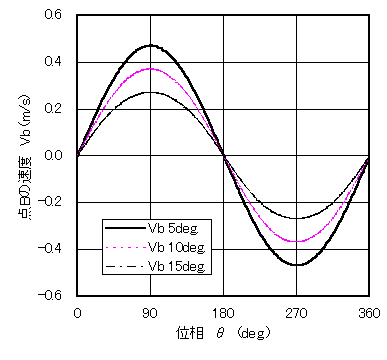
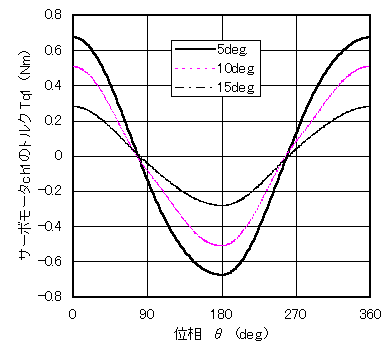
図2 正弦状の運動(ch1)
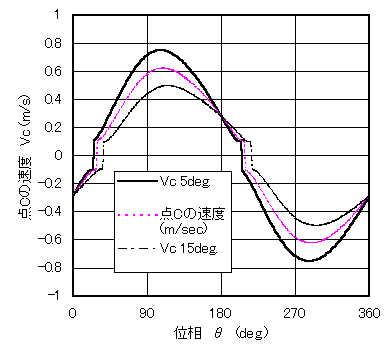
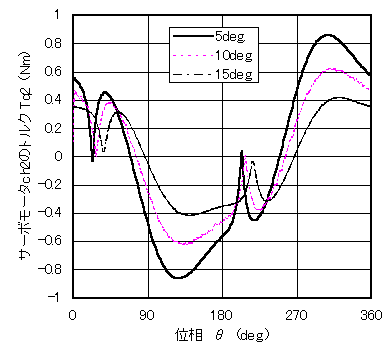
図3 正弦状の運動(ch2)
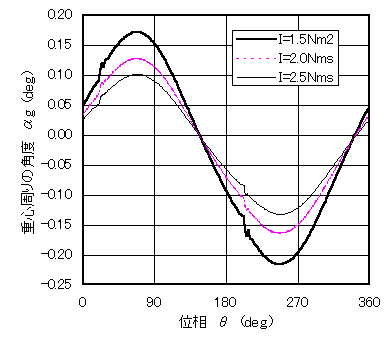
図4 重心周りの角度(静的)
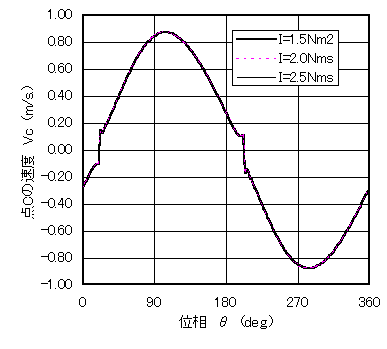
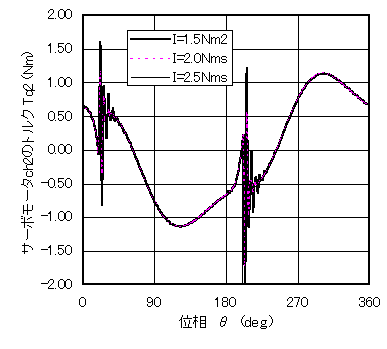
図5 速度とトルク(静的)
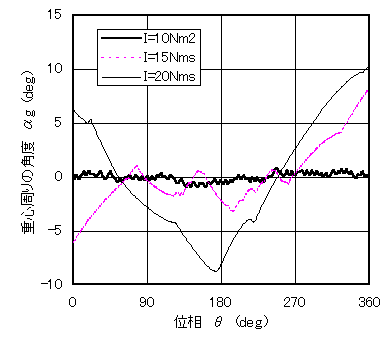
図6 重心周りの角度(動的)
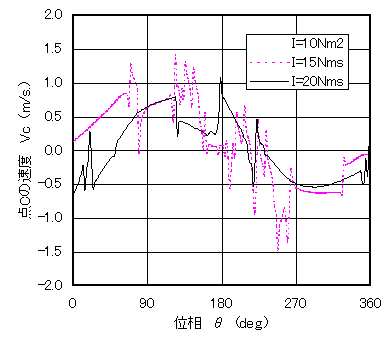
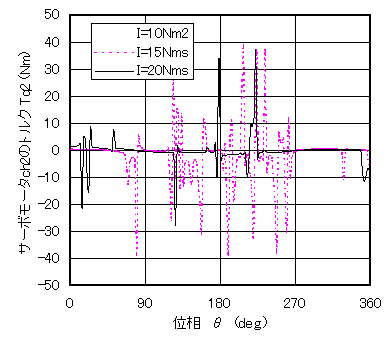
図7 速度とトルク(動的)
魚ロボットの重心周りの回転運動を含めた解析モデルを構築しましたが、残念ながら、適切な解を得ることはできませんでした。特に運動方程式を用いた場合、速度が0となる付近での計算に問題があります。また、上記の計算は機械設計を前提としており、流体力学的な荷重を考慮していません。今後、計算手法を検討するとともに、推進力、魚ロボットの速度、流体抵抗等を詳細に考慮することで、魚ロボットの運動をシミュレートできるものと考えられます。
Koichi Hirata
e-mail: khirata@nmri.go.jp (Office)
e-mail: khirata@gem.bekkoame.ne.jp (Home)