|
機械設計のための基礎製図
第8章 展開図と相貫図
 8.1 展開図 8.1 展開図
展開図とは,立体図形の全ての面を一平面上に表した図面のことである。簡単なものでは,図8.1に示すような正六面体や正四面体,正八面体の展開図はよく知られており,機械工学科の学生であれば誰でもが理解できるであろう。
|
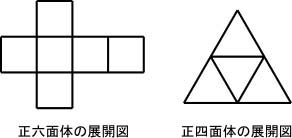
図8.1 正多面体の展開図
|
 展開図の例 展開図の例
身近な展開図として,段ボール箱や金属製の箱などがある(図8.2)。これらは1枚の紙あるいは金属板を折り曲げて作られている。また,プレス機械と呼ばれる機械加工では,1枚の金属板から様々な形状の製品が作られる(図8.3)。プレス加工において,展開図は重要である。
|

(a) 段ボール箱
|

(b) アルミニウム合金製ケース
|
図8.2 様々な展開図

図8.3 プレス加工で作られた製品
|
 8.2 展開図の描き方 8.2 展開図の描き方
ここでは,互いに45°の角度で曲がる直角エルボの展開図を作図例を紹介する。エルボとは,ある角度で交わる管の継ぎ手である(図8.4)。
|
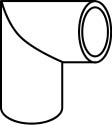
図8.4 直角エルボ
|
 【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。 【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。
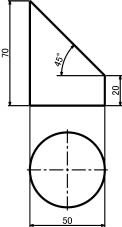
(1) 45°の角度で切断された直径50 mmのエルボを描く。
|
|
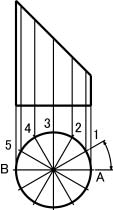
(2) 円を30°おきに12等分する。
(3) 等分された点(A,B,1~5)から上に垂線を引く。
|
|
(4) 正面図(台形)の真横に円周の長さ(50×3.14=157mm)の直線を引く。
(5) 直線を12等分する。
|
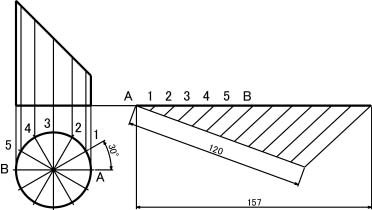
|
(6) 等分された直線から上に垂線を引き,それぞれ 対応する点を求める。
|
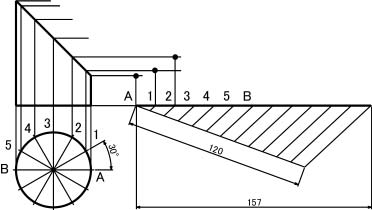
|
(7) 得られた点を滑らかに結び,完成させる。
|
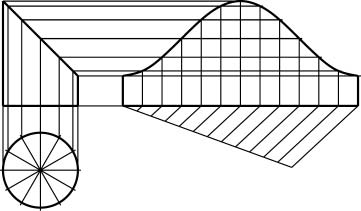
|
 8.3 相貫図 8.3 相貫図
相貫線とは,2つ以上の立体が交わる部分の線のことである。立体の平面同士が交わる場合,相貫線は直線になるため,相貫線の作図は容易である(図8.5)。しかし,平面と曲面あるいは局面同士が交わる場合,相貫線は曲線になり,その作図は著しく複雑になる。
|
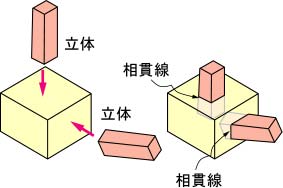
図8.5 平面同士の簡単な相貫
|
 相貫図の例 相貫図の例
身近な相貫として,自転車のフレームや配管部品などがある(図8.6)。このようなものの図面を描く場合には,相貫図の作図法をしっかりと習得しておく必要がある。また,特殊な例であるが,図8.7に示す魚ロボットの関節部分では曲面同士が交わっている。関節部分は運動するため,それぞれの部品の干渉を防ぐためにも,設計時には相関図の作図が重要である。
|

(a) 自転車
|

(b) 配管部品
|
図8.6 様々な相貫線

図8.7 魚ロボットの関節部
|
 8.4 相貫図の描き方 8.4 相貫図の描き方
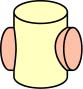
ここでは,円柱同士の相貫図の作図法を紹介する。このような曲面の相貫線を作図する際には,図8.8に示すように立体が交わる部分を直線平行面で切断し,交点を求めるという手順を行う。
|
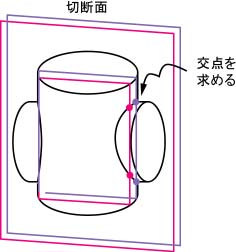
図8.8 円柱同士の相貫
|
 【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。 【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。
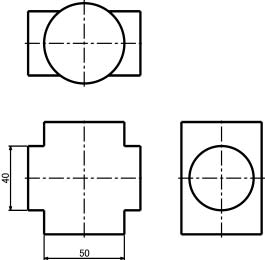
(1) 直径50mmと直径40mmの円柱の三面図を描く。
|
|
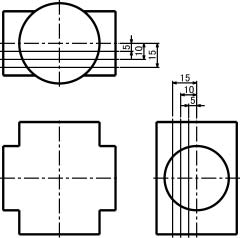
(2) 直径40mmの円柱の中心から,5mm,10mm,15mm切断面を描く。
|
|
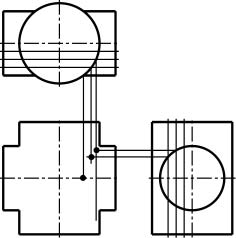
(3) 各切断面の交点を求める。
|
|
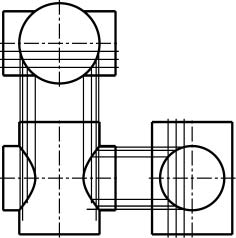
(4) 得られた交点を滑らかに結び,完成させる。
|
|
 8.5 課題 8.5 課題
【課題①】8.2節の手順に従って,直径50 mmの直角エルボの展開図を作図しなさい。
【課題②】8.4節の手順に従って,直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。
|
【課題③】次の図を参考にして,各自のアイデアでペーパークラフトの型紙を
作成しなさい。
●1個以上の立体があるペーパークラフトとする。
●直方体だけの作品は不可とする。
●組み立てることを考えて,のりしろもつけること。
|
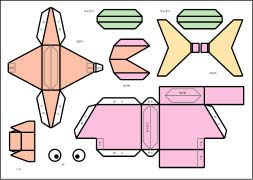
魚のペーパークラフト
|
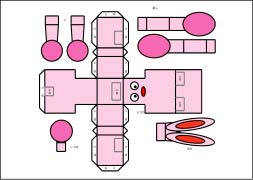
うさぎのペーパークラフト
|
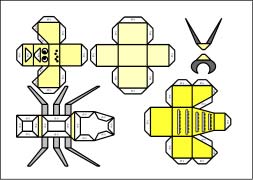
ありのペーパークラフト
|
【課題④】右図に示す円錐と正六角柱の相貫図を作図しなさい。
●六角ボルトの頭部や鉛筆の先端をイメージするとよい。
●円柱の相貫と同様,立体が交わる部分を直線平行面で切断し,交点を求める。
|
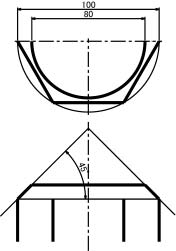
円錐と正六角柱の相貫
回答はこちら
|
|
 8.1 展開図
8.1 展開図 8.2 展開図の描き方
8.2 展開図の描き方 【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。
【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。 8.3 相貫図
8.3 相貫図 8.4 相貫図の描き方
8.4 相貫図の描き方 【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。
【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。 8.5 課題
8.5 課題 8.1 展開図
8.1 展開図 8.2 展開図の描き方
8.2 展開図の描き方 【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。
【例題】次の手順で直径50 mmの直角エルボの展開図を作図しなさい。 8.3 相貫図
8.3 相貫図 8.4 相貫図の描き方
8.4 相貫図の描き方 【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。
【例題】次の手順で直径50 mmと直径40 mmの円柱の相貫図を作図しなさい。 8.5 課題
8.5 課題