|
機械設計のための基礎製図
第5章 斜投影と等角投影
 5.1 立体図の必要性
斜投影図や等角投影図などの立体図は，第三角法による図面ほど正確な表現力はない。しかし，物体を立体的に表すことができ，実際の形をイメージするのが容易であるため，機械の説明図などによく使われている。
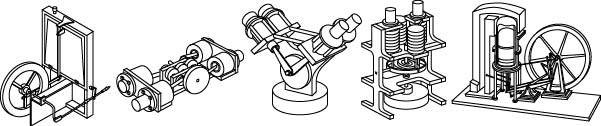
図5.1は，模型スターリングエンジンの外観，三面図（組立図）並びに立体図を示している。同図(c)の立体図は，(b)の三面図よりも模型スターリングエンジンの形状をよく表していると言える。しかし，この立体図からは，エンジンの構成部品や部品形状を推測することはできない。実際に部品を加工したり，あるいは組立をしたりする場合には，適切な三面図が必要である。
図5.1 模型スターリングエンジンの外観と図面
 立体図を簡単に描く方法
厳密なルールが決められた斜投影図や等角投影図について説明する前に，立体図を簡単に作図する方法とその要点を紹介する。
|
要点@：3本の軸（x，y，z）を決める。
最初に，横幅方向（x），奥行き方向（y），高さ方向（z）の3本の軸を決める。軸の角度は物体を見る方向で決まるが，z軸は鉛直方向とするとよい。なお，斜投影や等角投影では軸の角度が決まっている（右図）。
|
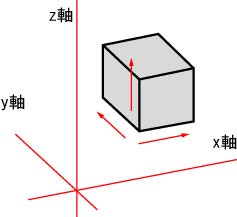
基本となる3本の軸
|
3本の軸の平行線を利用して，簡単に板材（直方体）を作図できる（右図）。
|
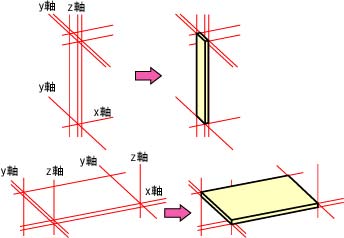
直方体の作図
|
要点A：「円」を楕円で表す。
機械部品は，板材と丸材（円柱）で構成されることが多い。円を斜め上方から見ると楕円になるので，円柱の立体図は楕円を利用する（右図）。手書きで厳密な楕円を作図するのは難しいが，パソコンを使えばそれほど難しくない。
水平移動した2つの楕円を2本の直線で結び，不要な線を消せば，簡単に円柱を作図できる。
楕円の中心位置さえわかれば，2つの円柱で構成されている部品を作図するのも難しくない。ただし，不要な線を消すのがやや複雑になる。
|
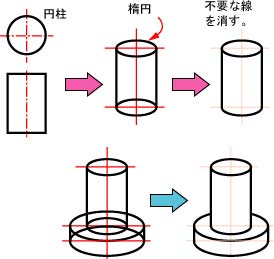
円柱の作図
|
要点B：z軸以外の円柱は，楕円を回転させる。
z軸を中心軸とした円柱は上記の方法で作図できる。z軸以外を中心軸とする円柱は，z軸を中心軸とした円柱を一連の図面ごと回転させればよい。例えば，y軸が中心軸となる場合，右図のように「円柱」回転させる。
|
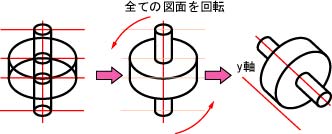
傾いた円柱の作図
|
以上の板材と円柱の作図を組み合わせれば，一見複雑に見える機械でも簡単に立体図を描くことができる。右図の模型スターリングエンジンの立体図では，3本の軸を利用して板材が作図されており，楕円と直線の組み合わせで円柱形状の部品が描かれている。
|
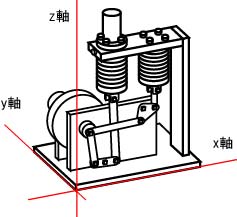
模型スターリングエンジンの立体図
|
スターリングエンジンの立体図
立体図は“もの作り”の構想段階で有効？
実際に1つの機械を作り上げていく場合，設計コンセプトの設定から始まり，機能分析，目的達成のための手段の検討，構造・形式の決定，寸法の決定，そして試作（機械加工）へと進んでいく。立体図（スケッチ）は，機械の形式を検討する際，特に有効である。イメージしたものを簡単に立体図にすることができれば，その後の寸法決定などの設計・製図にとても役立つ。
|
下図は，スターリングエンジンを搭載した模型ボートを試作する際に描いた立体図（スケッチ）である。このようなスケッチを描くと，自分の中でもイメージが明確になる。
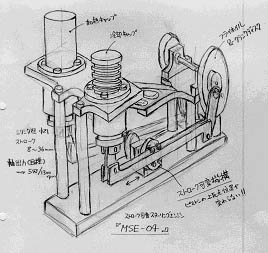
模型スターリングエンジンのスケッチ
|
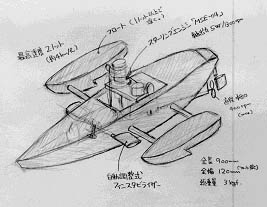
模型ボートのスケッチ
|
試作した模型スターリングボート
教材用エンジンの設計・試作（高温度差形）：日本機械学会, 「講習会：模型スターリングエンジンのつくり方と教育への利用」，2000．
立体図は機械の説明図などによく使われる
|
立体図は，実際の形をイメージするのが容易であるため，機械の説明図などによく使われる。
右図は，実験用スターリングエンジンのピストン部分を説明するための図面である。この例の場合，組み立てられたピストンを第三角法による二面図で表し，組立方法（部品の構成）を説明する図面を部品ごとの立体図で表している。
このような立体図は，自動車やバイクの説明書（サービスマニュアル）などでもよく見かける。
|
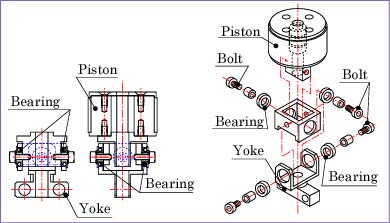
ピストンの説明図
|
5.2 斜投影
斜投影は，平行投影（平行光線を当てた投影）に含まれ，光線を投影面に傾けて投影する投影法である。光線の傾きによって様々な斜投影図を描くことができるが，最も一般的な斜投影では，正面図に対して45°の角度で光線を投影する。すなわち，図5.1に示すように，斜線の角度は正面図に対して45°となる。また，斜線の長さは，実寸の1/2とすることで，実際に目で見た形状を立体図に表すことができる。
|
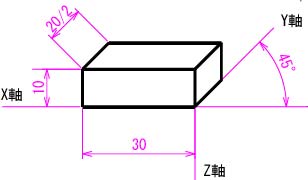
図5.2 直方体の斜投影図
|
5.3 等角投影
等角投影は，平行投影（平行光線を当てた投影）の一つである。光線は投影面に直交して投影されるが，物体の角度を傾ける点が第三角法などの正投影と異なる。図5.2に示すように，立体の3本の軸（X軸，Y軸，Z軸）が全て120°であることから等角図と呼ばれる。等角図は，辺の長さを実寸とすると，実物より大きく描かれるため，厳密な等角投影図では対角線の長さが実寸となるように描くとよい（教科書p.33，図3-29(c)，(d)参照）。ただし，本講義においては辺の長さを実寸としてよい。
|
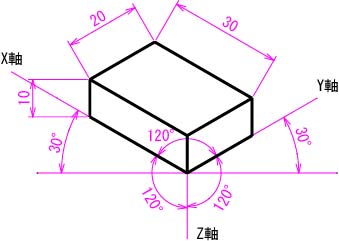
図5.3 直方体の等角投影図
|
5.4 課題
【課題@】直方体（幅30mm×高さ10mm×奥行20mm）の斜投影図を作成しなさい。
●奥行き方向の長さを1/2とすることに注意！
|
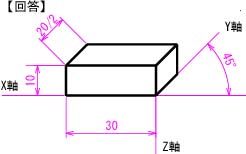
図1
|
【課題A】直方体（幅30mm×高さ10mm×奥行20mm）の等角投影図を作成しなさい。
|
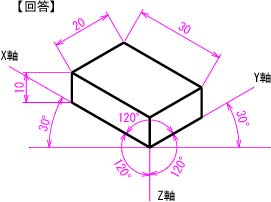
図2
|
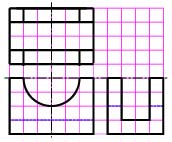
【課題B】図3の三面図から，斜投影図を作成しなさい。ただし，1目盛りを10mmとする。
図3
|
|
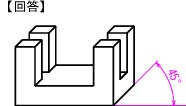
【課題C】図4の三面図から，等角投影図を作成しなさい。ただし，1目盛りを10mmとする。
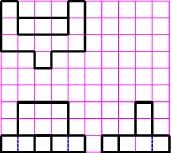
図4
|
|
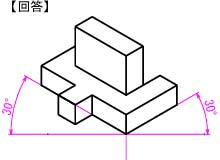
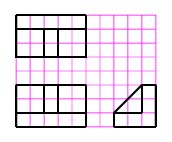
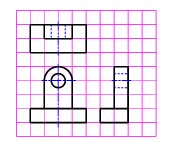
【課題D】図5の三面図から，斜投影図を作成しなさい。
【課題E】図6の三面図から，等角投影図を作成しなさい。
【課題F】図7の三面図から，斜投影図を作成しなさい。
●斜投影図と等角投影図を間違えないこと！
配布プリントのPDFファイル（平成14年度）
配布プリントのPDFファイル（平成13年度）
|
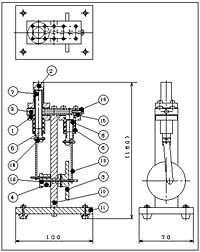
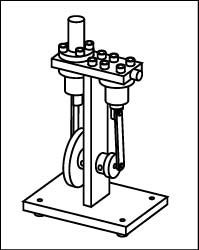(c) 立体図
