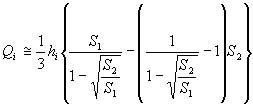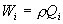実験用魚ロボット「UPF-2001」
胴体形状と流体特性
2001/11/15更新 平田宏一,河合秀祐

 胴体形状決定の要点
胴体形状決定の要点
魚ロボットの胴体形状は,遊泳速度等の推進性能に大きく影響します。もちろん,遊泳時の抵抗(水の抗力)ができるだけ小さくすることが望ましいのですが,実際には,構成部品の形状や寸法,重心や浮心の位置に制限を受け,流体力学的な検討だけで胴体形状を決定することはできません。魚ロボットの胴体形状を決める際の要点は以下の通りです。
①胴体形状が構成部品(各ユニット)の配置に適していること。
②体積(排水量)と全重量のバランスがとれていること。
③重心と浮心のバランスがとれていること。
④抵抗が小さいこと。
⑤尾ひれ周辺での流れの乱れが小さいこと。
⑥製作しやすい形状であること。
|
 胴体形状についての流体力学的考察
胴体形状についての流体力学的考察
 先端部の形状
先端部の形状
胴体先端部のとがった形状と丸い形状の相違について,流体力学的な観点から考えてみます(1)。図1(a)に示すように,とがった先端部が流れに対して傾いた場合,先端部で流れが剥がれてしまい,抵抗が大きくなります。一方,図1(b)のように先端部を丸い形状とした場合,先端部が流れに対して少し傾いても流れは剥がれにくく,抵抗は小さくなります。
尾ひれを左右に振動させて推進する魚ロボットは,遊泳中,頭部を左右に振ります。したがって,先端部の平面形状(上方から見た形状)は,丸い形状とするとよいと考えられます。
|
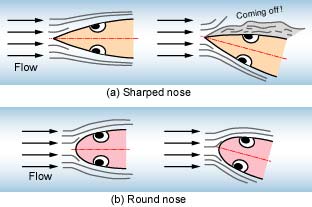
図1 先端部の形状
|
 流線形について
流線形について
周囲の流れが物体の後方まで乱れない形状を流線形と言います。流線形は抗力がとても小さく,魚ロボットの胴体形状に適していると言えます。流線形には様々な形状がありますが,その中でもよく知られた形状として,図2に示すフールマン(独)の流線形回転体があります(1)。フールマンは6種類の流線形回転体について抗力を測定し,基準面積当たりの抗力が最も小さい形状が図2(d)の形状であることを明らかにしました。そこで,魚ロボットUPF-2001の平面形状(上方から見た形状)を図2(d)の形状を参考にすることとし,各ユニットの寸法・形状に合わせて長さ方向並びに幅方向に調整することにしました。また,側面形状(横から見た形状)は,各ユニットの形状と重心位置を考えて,図2(f)の形状を上下それぞれに分割し,調整することとしました(図3参照)。
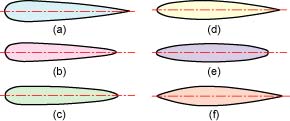
図2 フールマンの流線形回転体
|
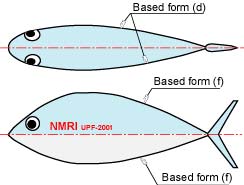
図3 魚ロボットUPF-2001の胴体形状
|
|
なお,超音速飛行機などでは,先端と後端がとがったレンズ形(あるいはダイヤモンド形)の胴体や翼が使われています。そのような形状は,物体が音速を超えるような高い速度で運動する場合に必要な形状です。しかし,水中での音速は約1500 m/sであり(空気中では約340 m/s),魚ロボットの遊泳速度よりもはるかに高く,これらの形状を参考にすることはできないことは言うまでもありません。魚ロボットにおいては,その速度や大きさの比率並びに流れの形態を考えて,飛行機や船舶の形状よりも,図4に示すような飛行船の形状(1)を参考にするとよいと考えられます。また,飛行船において,その胴体の浮力(体積)と運動時の抗力との関係が性能向上に極めて重要であることも魚ロボットによく一致しています。
|
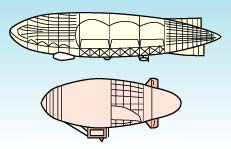
図4 飛行船の形状
|
 抵抗の概算
抵抗の概算
魚ロボットの胴体の抵抗を正確に推測することはとても難しいことです。以下では,とても簡易的な方法で抵抗を見積もることとします。
(1) レイノルズ数
流れの形態は,流体の粘性や密度,流れの速度,物体の大きさなどによって異なります。魚ロボットの抵抗を見積もる場合,次式に示すレイノルズ数Reを求めた後,その値に適した実験式や抵抗係数を用いる必要があります。
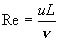
 (1) (1)
ここで,L[m]は代表長さであり,流線形の場合は一般に胴体(流線形)の全長をとります。ν[m2/s]は動粘性係数(水:ν=1.0×10-6m2/s)です。したがって,UPF-2001の場合,L =0.8 m,u=1~3 m/s程度ですので,レイノルズ数は,Re=8×105~2.4×106程度となります。
(2) 抵抗係数
抵抗FD[N]は,抵抗係数CD,密度ρ(水:ρ=1000 kg/m3),遊泳速度u[m/s]及び代表面積S [m2]を用いて,次式で整理されるのが一般的です。
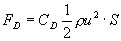
 (2) (2)
ここで,代表面積Sには,物体や用途の代表的な寸法をとります。例えば,自動車の場合は流れに直角な最大断面積(正面投影面積),飛行機の翼の場合は翼の面積をとるのが一般的です。流線形回転体の場合は正面投影面積や表面積をとることもありますが,魚ロボットの場合,胴体形状と体積との関係が重要ですので,体積Q [m3]の2/3乗を代表面積とするとよいと考えられます。
抵抗係数CDの値は代表面積Sの選び方によって異なります。図5は,いくつかの物体の抵抗を様々な代表面積を用いて換算した値を示しています(1)-(4)。
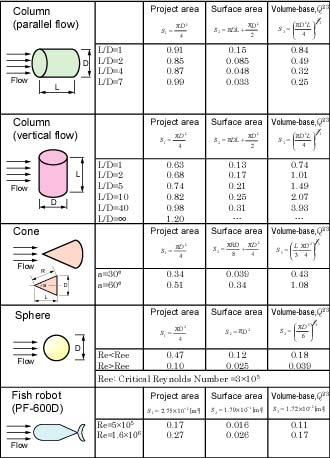
図5 物体の抵抗係数
(3) 流線形回転体の抵抗係数
図6は,図2に示したフールマンの流線形回転体における,Q2/3を代表面積とした場合の抵抗係数CDを示しています。これより,抵抗係数CDは0.02~0.04程度であり,図5の物体と比べてかなり小さいことがわかります。また,アボット(米)は,全長Lと直径Dとの比(細長比)をパラメータとして,流線形回転体の風洞実験を行いました。その結果,L/D=4.5において,抵抗係数CDが最も小さくなることがわかりました(1)。
以上のような検討により,魚ロボットの理想的な胴体形状を求めることができますが,上述した通り,実際の魚ロボットにおいては構成部品の形状などに制限を受けるため,理想的な流線形を採用するのはとても難しくなります。
|
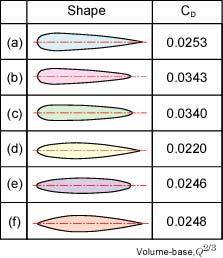
図6 流線形回転体の抵抗係数
|
(4) 魚ロボットUPF-2001の抵抗
以上の検討を踏まえて,魚ロボットUPF-2001の抵抗FD[N]を計算します。各寸法を検討した結果,胴体の全体積Qは20420 cm3程度であり,S=Q2/3=0.0747 m2であることが計算できました。図7は,抵抗係数CDをパラメータとし,遊泳速度u[m/s]を変化させた場合の抵抗FD[N]を示しています。例えば,CD=0.03とし,UPF-2001をu=3 m/sで遊泳させる場合,抵抗FDは約10 N(100 gf)です。これは,UPF-2001を3 m/sで遊泳させる場合,尾ひれによって約10 N(100 gf)の推進力が必要であることを示しています。
|
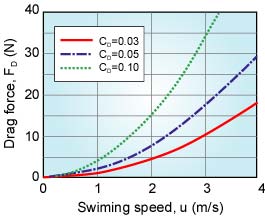
図7 魚ロボットUPF-2001の抵抗力
|
 排水量と重心・浮心位置の概算
排水量と重心・浮心位置の概算
 各ユニットの重量と重心位置
各ユニットの重量と重心位置
大まかな機械部品が完成した段階で,各ユニットの重量を測定しました。さらに,各ユニットの重心位置を推測し,全体の重心位置を計算しました。各ユニットをi=1,2・・・N,各ユニットの重量をMi,基準点からのx座標をxi,y座標をyiとすると,魚ロボットの全重量M及び魚ロボット全体の重心位置G(xG,yG)は次式で求められます。
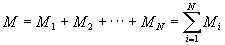
 (3) (3)
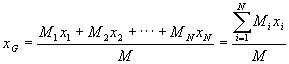
 (4) (4)
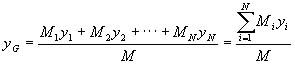
 (5) (5)
 胴体の浮心位置の概算
胴体の浮心位置の概算
胴体の浮心位置と重心位置が一致しないと,魚ロボットは水平姿勢を保てません。しかし,実際の魚ロボットを開発するに当たっては,胴体の加工精度や胴体材料(ウレタン,木材,接着剤,FRP)の密度(比重)が明確ではなく,製作する前に正確な浮心位置を見積もることはとても困難です。そのため,以下の手順で大まかな浮心位置を概算しました。
(1) 参考文献から魚ロボットの胴体に使用する流線形の座標を読みとります(図8,表1)。
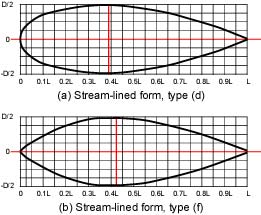
図8 流線形回転体の座標読みとり
|
表1 流線形回転体の座標

|
|
(2) 各ユニットの寸法・形状に合わせて,胴体形状の細長比L/D(全長Lと直径Dの比)を設定します。UPF-2001においては,全長L=800 mmとし,平面形状の相当直径Db=200 mm,側面形状上側の相当直径Dau=360 mm,側面形状下側の相当直径Dad=260 mmとしました(図9参照)。なお,胴体形状を検討する際,CAD図面の他,図10に示すような3種類のモデルを製作しました。
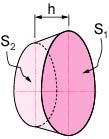
(3) 図9に示すように,魚ロボットの胴体をN分割し,各断面iが上側半径aui,下側半径adi,横側半径biの楕円になるように設定します。
|
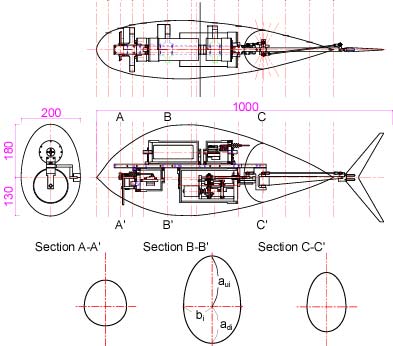
図9 魚ロボットUPF-2001の断面形状
|
|
(4) 半径a,bの楕円の面積はabπですので,各断面積Siを次式で求めます。
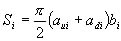
 (6) (6)
|

図10 魚ロボット胴体のモデル
|
(6) 次式により,全体積Q[m3]及び全排水量W[kgf]を求めます。
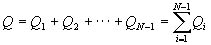
 (9) (9)
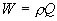
 (10) (10)
(7) 基準点から各体積Qiまでの代表距離(両断面の中点に近似)をxi'として,次式により浮心位置G'(xG',yG')を求めます。
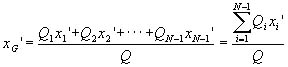
 (11) (11)
 UPF-2001の重心位置と浮心位置の計算結果
UPF-2001の重心位置と浮心位置の計算結果
|
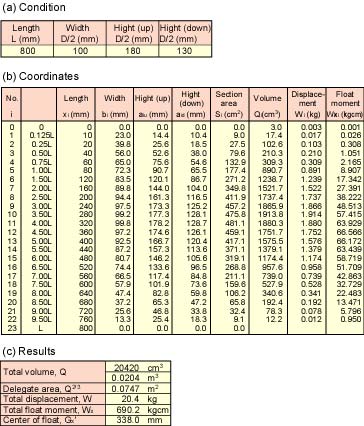
表2及び図12に各ユニット重量の測定結果並びに計算結果,表3に浮心位置並びに排水量の計算結果を示します。胴体の排水量は20.4 kgfであり,機械部品の全重量が6.1 kgfであるのに対してかなり大きい値です。しかし,全重量に胴体材料の重量が含まれていないことや,胴体全体が水密でなく胴体上部にだけ浮力材を挿入することを考えると妥当な値であると考えられます。また,x軸方向(長さ方向)の重心位置xGが346 mmであるのに対し,浮心位置xG'は338 mmです。これは,バランサ(おもり)を取り付けることで十分に調整できる範囲です。
なお,詳細なバランスを考える場合,y軸方向のyG'とyGとの大小関係(上下関係)を確認する必要がありますが,UPF-2001においては明らかにyG'>yG(上向きを正)ですので,yG'を計算していません。
|
表2 各ユニット重量の測定・計算結果
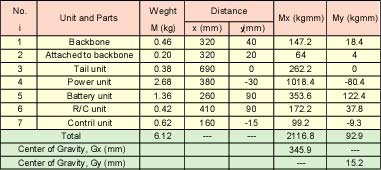
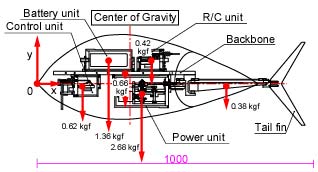
図12 魚ロボットの重心位置
|
表3 浮心位置並びに排水量の計算結果
 まとめ
まとめ
以上,魚ロボットの胴体形状について,流体力学的検討並びに形状決定の手順について説明しました。流体力学的な検討はとても簡易的なものですが,遊泳している魚ロボットの挙動は複雑であり,詳細な解析をしたとしても必ずしも高性能な魚ロボットを開発できるとは限らないと考えています。また,重心や浮心の計算においても,かなり大きい計算誤差が含まれていますが,最終的にバランサで調整することを前提とした魚ロボットの開発過程においては十分な精度であると考えています。
 参考文献
参考文献
(1) 牧野光雄:流体抵抗と流線形,産業図書(1991).
(2) 冨田幸雄:水力学,p.157,実教出版(1993).
(3) 機械学会:機械工学便覧,A5,p.97-106,丸善(1987).
(4) 瀧本忠教,平田宏一,牧野雅彦:魚ロボットの抵抗測定と流体力学的検討,日本設計工学会東北支部,平成12年度研究発表講演会,p.84-87(2000).
[UPF-2001]
[Experimental Fish Robots]
[ Fish Robot Home Page ]
[ Power and Energy Engineering Division ]
[ Hirata HOME ]
[ NMRI HOME ]
| 
 胴体形状決定の要点
胴体形状決定の要点 胴体形状についての流体力学的考察
胴体形状についての流体力学的考察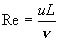
 (1)
(1)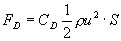
 (2)
(2)
 排水量と重心・浮心位置の概算
排水量と重心・浮心位置の概算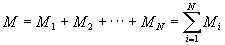
 (3)
(3)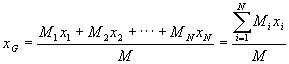
 (4)
(4)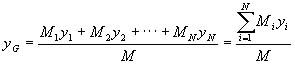
 (5)
(5) 胴体の浮心位置の概算
胴体の浮心位置の概算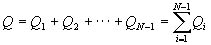
 (9)
(9)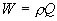
 (10)
(10)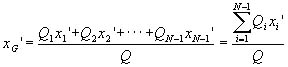
 (11)
(11) UPF-2001の重心位置と浮心位置の計算結果
UPF-2001の重心位置と浮心位置の計算結果
 まとめ
まとめ 参考文献
参考文献







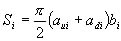
 (6)
(6)