実験用魚ロボット「UPF-2001」
パワーユニットの詳細
2001/11/26更新 平田宏一,河合秀祐

 基本構造と特徴
基本構造と特徴
魚ロボットUPF-2001のパワーユニットは,(i) 動力源である直流モータ,(ii) 直流モータの回転運動を減速するための歯車機構,(iii) 減速された歯車の回転運動を往復運動に変換するスコッチ・ヨーク機構,(iv) ユニット内を水密とするためのシール機構,(v) 往復運動を尾部へと伝えるための連結機構から構成されています。表1はパワーユニットの主な仕様を示しています。
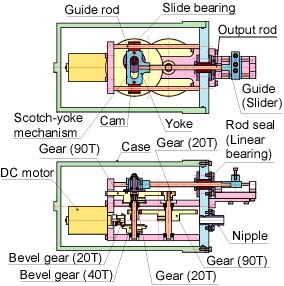
図1 パワーユニット
画像をクリックすると,大きい画像が見られます。
|
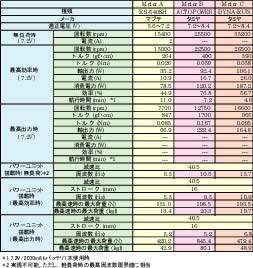
表1 パワーユニットの仕様
画像をクリックすると,大きい画像が見られます。
|
 小型・高出力な直流モータ
小型・高出力な直流モータ
UPF-2001の動力源には市販のラジコン模型用直流モータを使用しています。直流モータは,R/Cサーボモータやパルスモータと比べて,小型・高出力で扱いやすいという特徴があります。また,様々な出力レベルの直流モータが市販されているので,出力や周波数の点で問題になることはほとんどありません。しかし,後述するような,回転運動を減速する機構や往復運動に変換する機構が必要になります。なお,UPF-2001のパワーユニットでは,異なる特性を持つ3種類の直流モータを準備しています(表1,表2参照)。
|

図2 直流モータ
|
 歯車を用いた減速機構
歯車を用いた減速機構
小型・高出力な直流モータは,10000 rpm(167 Hz)以上という,かなり高い回転数で運転しますので,そのままの回転数で尾ひれを動かすことはできません。そのため,直流モータの回転運動を減速するための機構が必要になります。UPF-2001では,6枚の歯車を組み合わせて,1/40.5の回転数に減速しています。
|

図3 歯車を用いた減速機構
|
 スコッチ・ヨーク機構
スコッチ・ヨーク機構
回転運動を往復運動に変換する機構には,スコッチ・ヨーク機構を採用しました。右図に示すスコッチ・ヨーク機構は,クランクディスクの偏心させた位置に回転軸を取り付け,長穴をあけたヨークを往復運動させます。往復運動のストロークはクランク半径を変更することで調整できます。UPF-2001では,ストロークを16 mmとしています。ヨークに直動玉軸受を取り付けていますので,シール機構に無理な力がかかりにくい,理想的な直線運動を実現しています。
|

図4 スコッチ・ヨーク機構
|
 水密のためのシール機構
水密のためのシール機構
UPF-2001の往復動シールには市販の直動軸受(ASK社)を使用しています。そのシール面はPTFE(テフロン)なので,出力軸のサイドスラスト(横向きの力)をできる限り押さえる必要があります。上述のスコッチ・ヨーク機構や後述の連結機構はサイドスラストを押さえるために有効です。なお,直流モータと歯車,スコッチ・ヨーク機構全体を覆うケースはゴム製のOリングで水密されています。
|

図5 シール機構
|
 尾部への連結機構
尾部への連結機構
図6は往復運動を尾部へと伝えるための連結機構です。PTFE製の直動軸受を痛めないようするため,ガイドを取り付けています。
|

図6 尾部への連結機構
|
 設計計算の概略
設計計算の概略
直流モータの出力を尾ひれの運動に伝えるためには,魚ロボットの寸法,直流モータの出力レベル,歯車の減速比などを適切に設定する必要があります。以下,尾ひれに作用するトルクや直流モータに必要な出力,歯車の減速比を決めるための簡易的な計算方法を紹介します。
 最大トルクの計算式
最大トルクの計算式
図7の計算モデルに示すように,振動する尾部を1枚の平板に置き換えます。平板の重心をG,関節から重心Gまでの距離をr(m),尾ひれの片側振幅A(deg),尾ひれの周波数をf(Hz),時間をt(s)とすると,尾ひれが正弦状に運動する場合,重心Gの変位xG(m)は次式で近似できます。
|
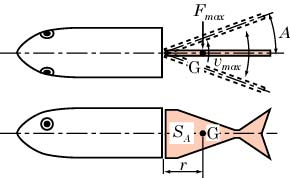
図7 計算モデル
|
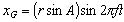
 (1) (1)
したがって,重心Gの速度vG(m/s)は次式で表されます。
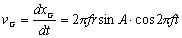
 (2) (2)
速度vGは,cos2πft=1のとき(尾ひれが中心線上を通過するとき)に最大vGmaxとなり,次式で表されます。
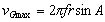
 (3) (3)
重心Gに作用する最大荷重FGmaxは平板の面積SAを用いて次式で計算されます。
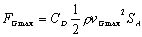
 (4) (4)
ここで,CDは平板の抵抗係数(CD =1.2),pは水の密度(p=1000 kg/m3)です。
したがって,関節に作用する最大トルクTqmax(Nm)は次式で求められます。
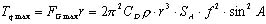
 (5) (5)
以上の計算式によって,魚ロボットの尾ひれを運動させる場合の最大トルクを求めることができます。
一方,直流モータのトルクをTqmot(Nm),歯車の減速比をDとすると,直流モータが駆動できる関節のトルクはTqmot/D(Nm)となります。したがって,Tqmax<Tqmot/Dが直流モータで動かすことができる範囲となります。
 平均出力の計算式
平均出力の計算式
魚ロボットの尾ひれを安定して運動するためには,最大トルクと同様,平均出力の計算が必要になります。以下,最大トルクと同様な簡易的な方法で平均出力を求めます。
重心Gの1周期当たりの移動距離は約4rsinA(m)であるので,平均速度vm(m/s)は次式で表されます。
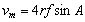
 (6) (6)
式(4),(5)の最高速度vGmaxを平均速度vmに置き換えて,平均荷重Fm及び平均トルクTqmを求めると,次式となります。
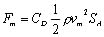
 (7) (7)
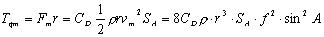
 (8) (8)
したがって,平均出力Wm(W)は次式で求められます。
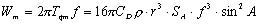
 (9) (9)
式(9)で求められる平均出力Wm(W)が直流モータの出力を下回っている範囲で,尾ひれの安定した運動が可能となります。
 減速比の選定手順
減速比の選定手順
以上のようなトルクや出力を計算することで,魚ロボットの運動可能範囲を概ね推測することができます。同時に,大まかな魚ロボットの寸法や使用する直流モータを決定した場合,直流モータの回転数をどの程度減速するかを決める必要があります。以下,減速比Dの選定手順例を紹介します。
ラジコン模型用直流モータのカタログや説明書には,最高出力時の特性,最高効率時の特性及び無負荷時の特性などが表示されています(表1)。それぞれの特性における回転数(Hz)をfP(最高出力時),fE(最高効率時),fN(無負荷時),トルクをTqP(最高出力時),TqE(最高効率時),TqN(無負荷時=0)とすると,
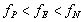
 (10) (10)
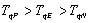
 (11) (11)
となります。トルクが回転数の上昇に伴って直線的に減少すると仮定した場合,最高出力時の回転数fPは無負荷時の回転数fNの1/2となります。そして,ラジコン模型用直流モータにおいて,最高効率時の回転数fEは,最高出力時の回転数fPよりもかなり高く,無負荷時の回転数fNに近いという特性があります。このような直流モータを魚ロボットに適用する場合,fP〜fEの範囲で定格運転できるように,減速比Dを選定します。尾ひれの周波数fと直流モータの任意の回転数fmot(Hz)との関係は,f=Dfmotですので,
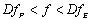
 (12) (12)
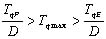
 (13) (13)
を満たすように減速比Dを決めればよいことになります。一方,式(3)〜(7)を用いると,トルクTqmot,fmot,r,A,SA及びDの関係式が導かれます。例えば,減速比Dについて整理すると次式が得られます。
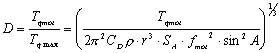
 (14) (14)
したがって,式(13)より,
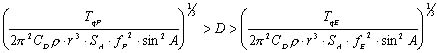
 (15) (15)
が導かれます。
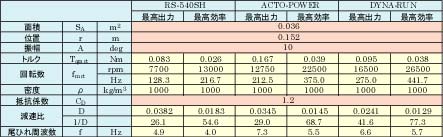
表2は,図2及び表1に示す3種類のモータを使用し,UPF-2001の寸法(r=0.152 m,SA=0.036 m2)に基づき,振幅A=10 degとして減速比Dを求めた結果です。これより,減速比1/40〜1/60程度が適当であることがわかります。このような計算結果や歯車の配置などを考慮して,UPF-2001におけるパワーユニットの減速比を1/40.5としました。
表2 減速比の計算結果
画像をクリックすると,大きい画像が見られます。
 計算結果
計算結果
図8は,UPF-2001の寸法に基づき,振幅Aを5,10及び15 degとした場合の尾ひれの周波数fに対する最大トルクTqmaxの計算結果を示しています。同図には,減速比D=1/40.5とした場合の直流モータのトルク(カタログ値)を併記しています。これより,最大トルクTqmaxは,周波数f及び振幅Aの増加に伴い,急激に増加することがわかります。同図において,最大トルクTqmaxの計算結果が直流モータのトルク特性を下回る範囲が,尾部の駆動可能範囲です。
図9は,周波数fに対する平均出力Wmの計算結果並びに直流モータの出力(カタログ値)を示している。図8と同様,尾ひれを動かすのに必要な平均出力Wmは,周波数f及び振幅Aの増加に伴い,急激に増加することがわかる。また,平均出力Wmの計算結果が直流モータの出力特性を下回る範囲が,尾部を安定して動かすことができる範囲です。
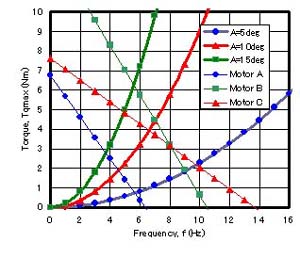
図8 トルクの計算結果
|
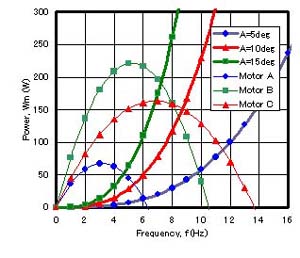
図9 出力の計算結果
|
これらの結果より,高トルク型のモータB(田宮製,ACTO-POWER)は尾ひれの振幅を大きくした場合に有効であり,高回転型のモータC(田宮製,DYNA-RUN)は尾ひれの振幅を比較的小さくし,高い周波数で運転するのに有効であると考えられます。また,標準型であるモータA(マブチ製,RS-540SH)は比較的消費電力が少ないため,長時間航行に適していると考えられます。
 まとめ
まとめ
以上,魚ロボットUPF-2001のパワーユニットについて説明し,その減速比や直流モータの選定方法について説明しました。以上の計算では,尾ひれを平板に置き換えていますが,実際の尾ひれは円柱または円すいに近い形状をしているため,抵抗係数に大きな違いがあると考えられます。さらに,遊泳している魚ロボットの尾ひれ周囲の水の流れは極めて複雑であり,一定の抵抗係数を与えるような計算が適当であるかどうかはわかりません。しかし,式(5)及び式(8)に示すように,尾ひれを動かすトルクが,周波数及び振幅の2乗に比例し,尾部の長さ(重心までの距離)の3乗に比例することなど,定性的な特性は十分に把握できるものと考えています。
[UPF-2001]
[Experimental Fish Robots]
[ Fish Robot Home Page ]
[ Power and Energy Engineering Division ]
[ Hirata HOME ]
[ NMRI HOME ]
| 
 基本構造と特徴
基本構造と特徴
 (1)
(1)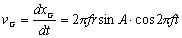
 (2)
(2)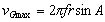
 (3)
(3)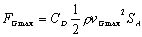
 (4)
(4)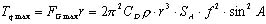
 (5)
(5)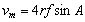
 (6)
(6)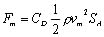
 (7)
(7)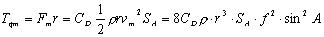
 (8)
(8)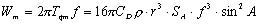
 (9)
(9)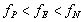
 (10)
(10)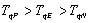
 (11)
(11)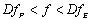
 (12)
(12)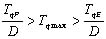
 (13)
(13)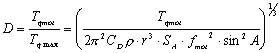
 (14)
(14)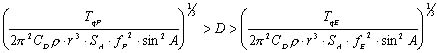
 (15)
(15)
 計算結果
計算結果 まとめ
まとめ








