Program to estimate wave-induced steady forces and moment on a ship

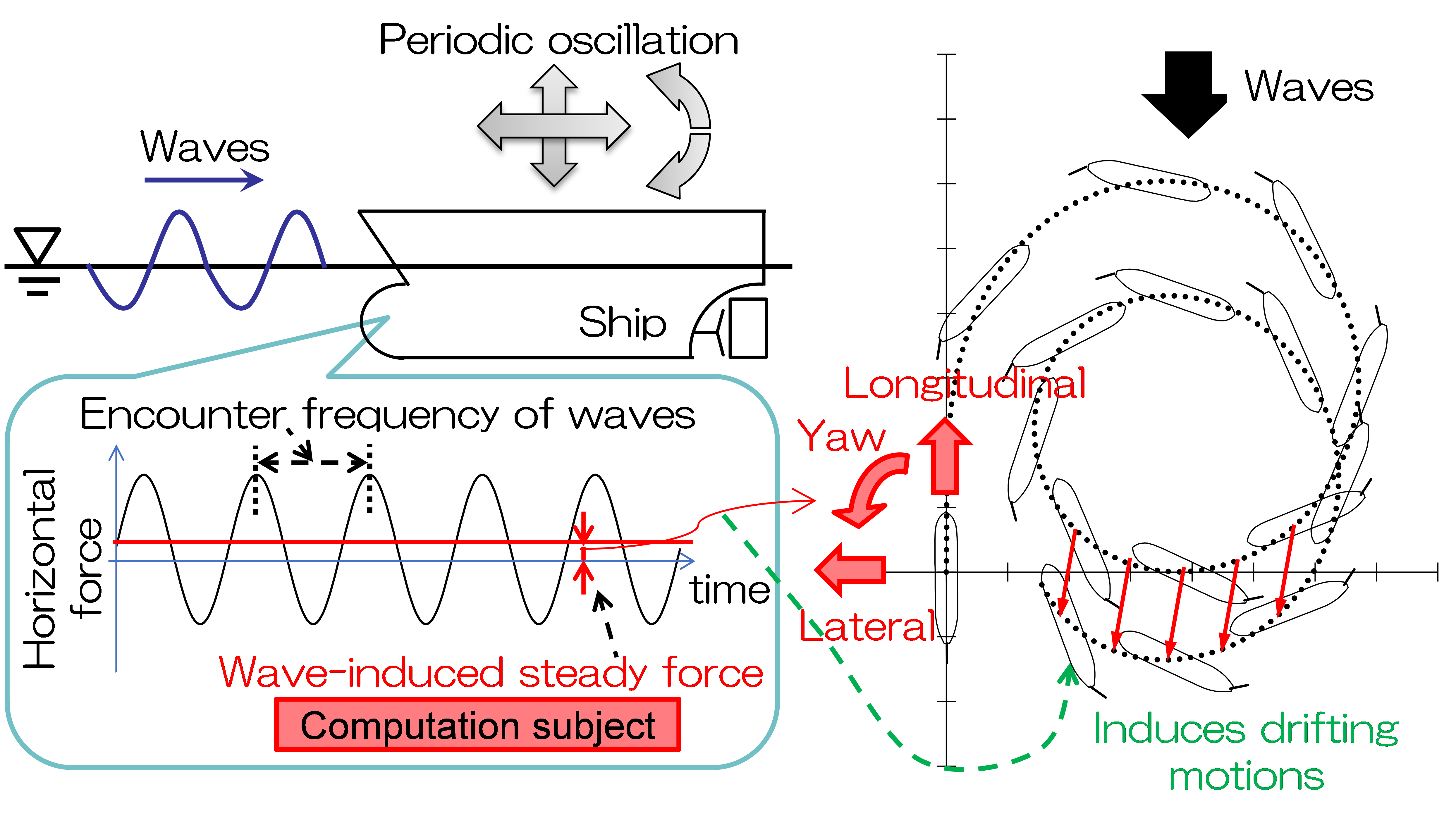
Fig. 1 Schematic diagram of wave-induced steady forces and moment on a ship and the influence on maneuvering motions

Ships navigating in waves create new unsteady waves, because they reflect and diffract incident waves as well as oscillate periodically in accordance with the wave crests and troughs. As a result, unsteady wave forces on the ship exhibits nonlinear natures, which can generate time-averaged steady components (see Fig.1). Although these steady components are higher-order compared to wave exiting forces, they induce a time-averaged decrease in the ship's speed, a ship’s lateral drift, and an increase in the rudder angle required to maintain the ship's course. Moreover, these steady components also affect the ship's position, heading, etc. as the integral values. Therefore, when evaluating ship's propulsion and maneuvering performance in actual seas, it is essential to consider the wave-induced steady forces and moment in the ship’s longitudinal, lateral and yaw directions. This program predicts such wave-induced steady forces theoretically and practically. We are currently developing a method to numerically simulate ship’s maneuvering motions in waves that takes into account the wave-induced steady forces predicted using this program.

• The computation program requires the following input data: ship's principal particulars, horizontal cross-section at the waterline, and shape of the hull submerged surface (offset table).
• The program outputs the following prediction results in regular waves: wave-induced steady forces and moment in ship's longitudinal, lateral and yaw directions and complex amplitudes of periodic oscillation with 5 degrees of freedom (sway, heave, roll, pitch, and yaw).
• The computation program is applicable to a wide range of wavelengths, from very short to long waves at arbitrary directions, such as head, beam, following waves.
• The effects of ship's forward speed are taken into account. Furthermore, the effects of ship's lateral drift are also considered in short waves. Thus, compilation under ship conditions that are closer to actual operation in a seaway can be performed compared to conventional prediction considering only the forward speed effects (see Fig.2).
• The wave-induced steady forces are computed using the combination of two different theoretical methods assuming a potential flow ^[1].
• The computation method has been validated through tank tests (see Figs. 3 and 4).

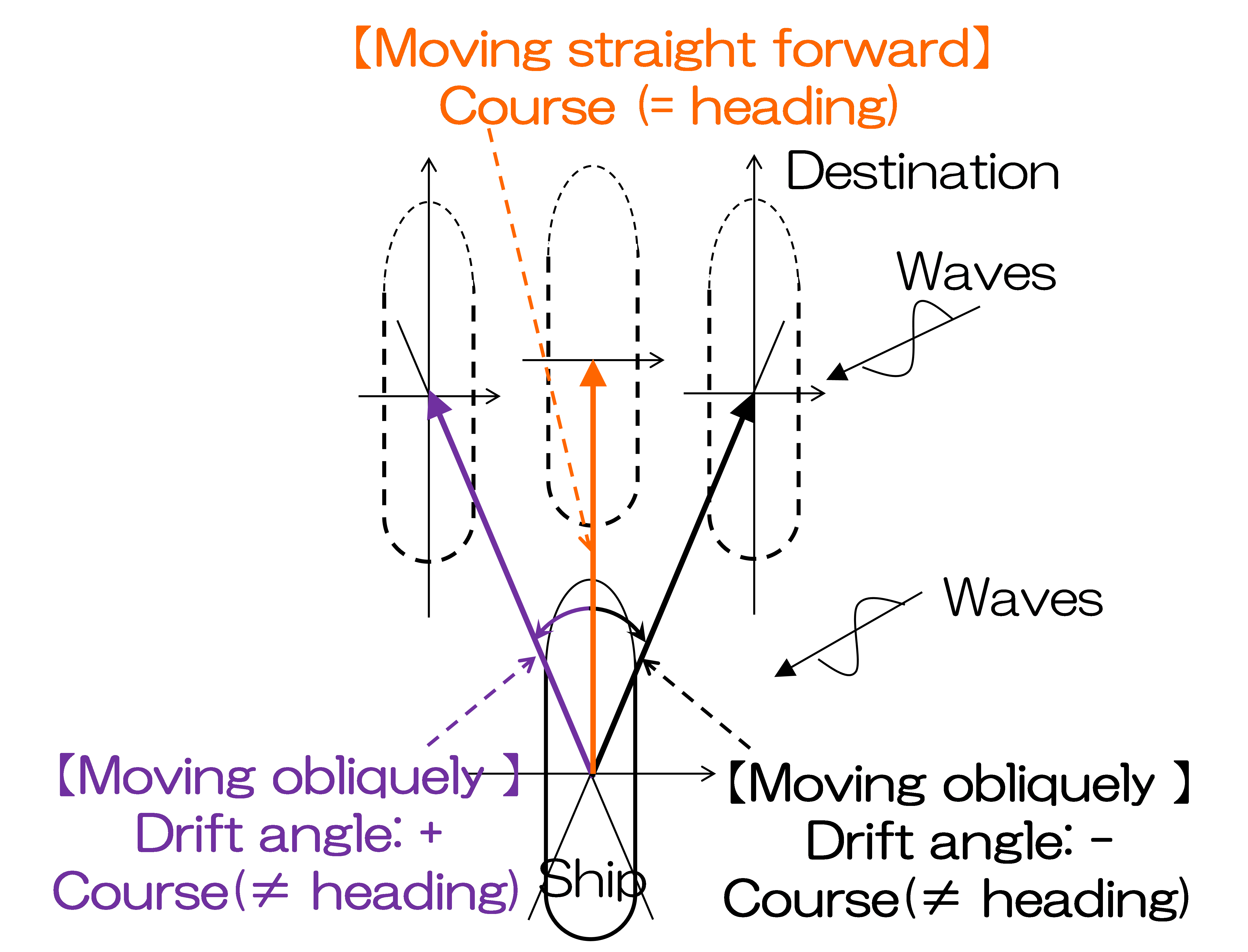
Fig. 2 Schematic diagram of different ship's conditions: resting, moving straight forward, and moving obliquely with lateral drift

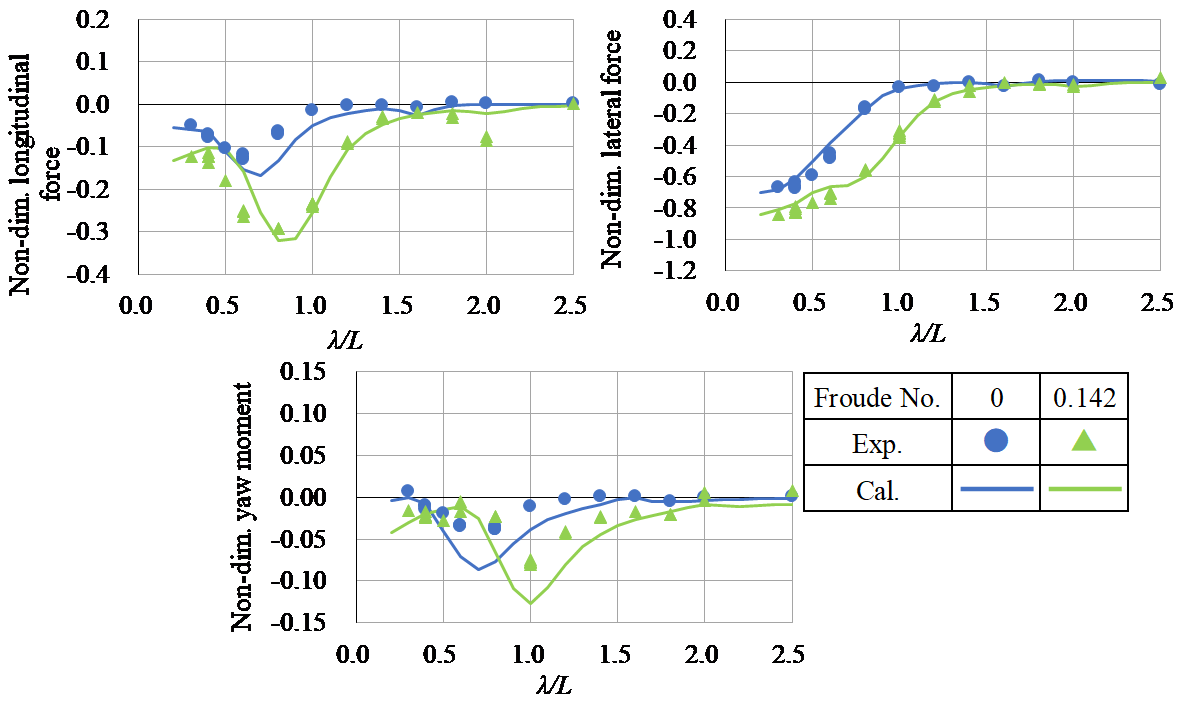
Fig. 3 Wave-induced steady horizontal forces and yaw moment on a very large crude carrier (VLCC) under resting and moving straight forward in oblique head waves, 60 deg. ^[1]

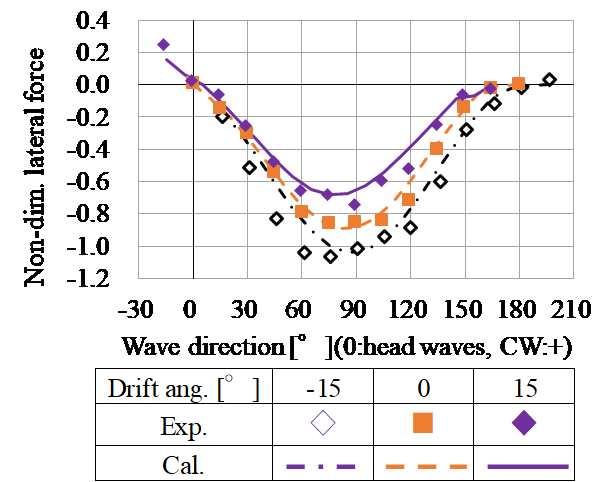
Fig. 4 Wave-induced steady lateral force on a VLCC under moving straight forward and obliquely with lateral drift in short waves (ratio of wavelength to ship length, λ/L, 0.4) ^[2]

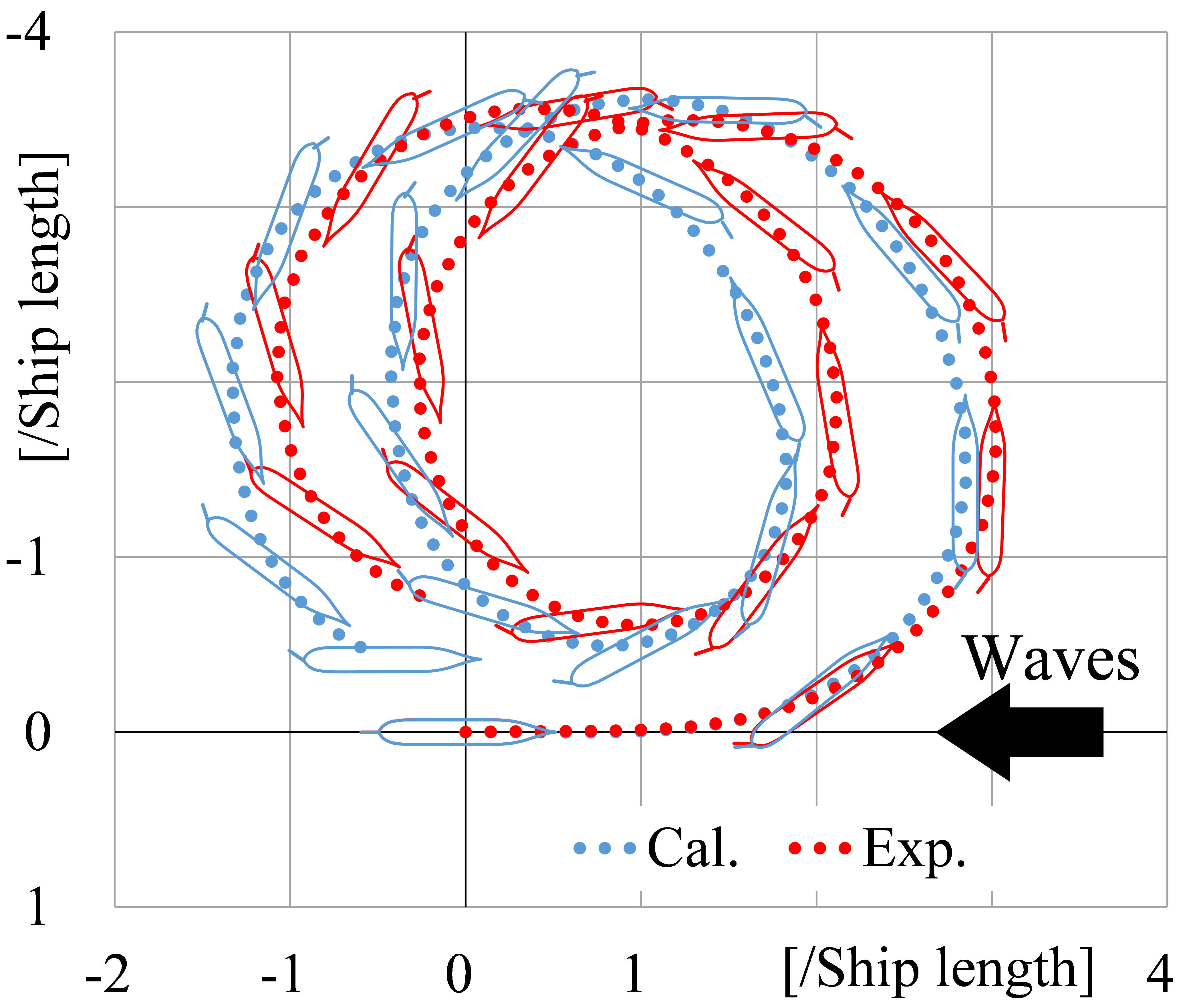
Fig.5 Trajectory of a container ship turning in regular short waves (λ/L, 0.5) and the time history of oscillatory motions (under development)

1. Suzuki, R. (2024) : A Practical Method of Predicting the Wave-induced Steady Forces and Yaw Moment Acting on a Ship Advancing in Oblique Waves, Proc. of 34th Int. Ocean & Polar Eng. Conf., Rhodes, Greece, ISOPE, pp.2248-2255
2. Suzuki, R., Ohashi, K., & Ueno M. (2023): Estimation of Steady Wave Forces and Moment Acting on an Obliquely Moving Ship in Short Waves, and Its Application in a Manoeuvring Simulation, Appl. Math. Model., Vol.125, Part A, pp.261-292.